Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-30T23:13:18.654Z Has data issue: false hasContentIssue false
  • English
  • Français

A semilinear elliptic eigenvalue problem, I

Published online by Cambridge University Press:  14 November 2011

Grant Keady  and
John Norbury
Grant Keady
Affiliation:
Mathematics Department, University of Western Australia
John Norbury
Affiliation:
St Catherine's College, Oxford
Get access Rights & Permissions [Opens in a new window]

Synopsis

The nonlinear operator equation (N), 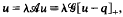, describes both semilinear elliptic boundary value problems (P) and their natural discretisations (Ph). (Here 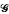is a positive compact linear operator and [t]+ ≡ (t + |t|)/2 for all t ∊ ℝ.) It is proved that, for q ≧ 0 (q ≢ 0), in a Banach lattice E the equation (N) has an unbounded continuum ℱ of nontrivial solutions (λ, ψ) ∊ ℝ × E bifurcating from infinity at (λ1, ∞) (here 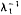is the first (positive) eigenvalue of 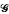). All nontrivial solutions (λ, ψ) have λ ≧ λ1, and if 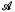maps a smaller cone Ks, into itself then there is a ℱs ⊂ℝ×Ks with similar properties to ℱ. The existence theory for (N) is applied to problems (P) and (Ph) which are defined on the simply-connected domain Ω. It is shown that the projection of ℱ on the λ-axis is either unbounded if the continuous function q > 0 except on a set of measure zero in Ω, or is bounded if q ≡ 0 on a subdomain of Ω. If 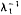is the second eigenvalue for 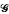in (Ph) then there is at most one nontrivial solution for each λ satisfying λ1 < λ < λ2; in the corresponding uniqueness result for (P) q is restricted to being strictly positive somewhere on ∂Ω Additional properties for the solutions of (P) and (Ph) are also proved.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 87 , Issue 1-2 , 1980 , pp. 65 - 82
Copyright
Copyright © Royal Society of Edinburgh 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Amann, H.. Fixed point equations and non-linear eigenvalue problems in ordered Banach spaces. SIAM Rev. 18 (1976), 620–709.CrossRefGoogle Scholar
2Berestycki, H. and Brezis, H.. Sur certains problèmes de frontière libre. C.R. Acad. Sci. Paris 283 (1976), 1091–1101.Google Scholar
3Budden, P. J. and Norbury, J.. A non-linear elliptic eigenvalue problem. J. Inst. Math. Appl. 24 (1979), 9–33.CrossRefGoogle Scholar
4Courant, R. and Hilbert, D.. Methods of Mathematical Physics, Vol. I (New York: Interscience, 1953).Google Scholar
5Dancer, E. N.. Global solution branches for positive mappings. Arch. Rational Mech. Anal. 52 (1973), 181–192.CrossRefGoogle Scholar
6Dugundji, J.. An extension of Tietze's theorem. Pacific J. Math. 1 (1951), 353–367.CrossRefGoogle Scholar
7Gradshteyn, I. S. and Ryzhik, I. M.. Tables of integrals, series and products (New York: Academic Press, 1965).Google Scholar
8Isaacson, E. and Keller, H. B.. Analysis of Numerical Methods (New York: Wiley, 1966).Google Scholar
9Keady, G. and Norbury, J.. A semilinear elliptic eigenvalue problem, II. The plasma problem. Proc. Roy. Soc. Edinburgh Sect. A 87 (1980), 83–109.CrossRefGoogle Scholar
10Krasnosel'skii, M. A.. Topological Methods in the Theory of Non-linear Integral Equations (Oxford: Pergamon, 1963).Google Scholar
11Krasnosel'skii, M. A.. Positive solutions of Operator Equations (Groningen: Noordhoff, 1964).Google Scholar
12Norbury, J.. Steady planar vortex pairs in an ideal fluid. Comm. Pure Appl. Math. 28 (1975), 679–700.CrossRefGoogle Scholar
13Puel, J.. Un problème de valeurs propres nonlinéaire et de frontière libre. C.R. Acad. Sci. Paris 284 (1977), 861–880.Google Scholar
14Rabinowitz, P. H.. Some global results for non-linear eigenvalue problems. J. Functional Analysis 7 (1971), 487–513.CrossRefGoogle Scholar
15Schaefer, H. H.. Banach Lattices and Positive Operators (Berlin: Springer, 1974).CrossRefGoogle Scholar
16Temam, R.. Remarks on a free boundary value problem arising in plasma physics. Comm. Partial Differential Equations 2 (1977), 563–586.CrossRefGoogle Scholar