Hostname: page-component-669899f699-cf6xr Total loading time: 0 Render date: 2025-04-30T02:47:20.571Z Has data issue: false hasContentIssue false
  • English
  • Français

The roles of nonlinear diffusion, haptotaxis and ECM remodelling in determining the global solvability of a cancer invasion model

Part of: Equations and systems of special type Parabolic equations and systems Physiological, cellular and medical topics

Published online by Cambridge University Press:  13 September 2024

Chunhua Jin
Chunhua Jin*
Affiliation:
School of Mathematical Sciences, South China Normal University, Guangzhou, 510631, China ([email protected])
*
*Corresponding author
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we consider the following PDE-ODE system modelling cancer invasion with slow diffusion and ECM remodelling,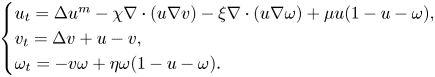

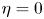\[ \begin{cases} u_t=\Delta u^m-\chi\nabla\cdot(u\nabla v)-\xi\nabla\cdot(u\nabla\omega)+\mu u(1-u-\omega), \\ v_t=\Delta v+u-v, \\ \omega_t={-}v\omega+\eta \omega(1-u-\omega). \end{cases} \]
For the special case $\eta =0$, fruitful results have been achieved since Tao and Winkler's work in 2011. However, there is no any progress for the general case $\eta >0$ 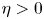in the past ten years. In this paper, we analysed some commonly used research methods when $\eta =0$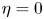, and found that these methods are completely unsuitable for situations where $\eta >0$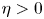. By introducing some new forms of functionals, we reconstruct the relationship between the haptotactic term and the nonlinear diffusion term, and ultimately prove the global existence of weak solutions. This result improves and perfects a series of works previously presented in the literature.

Keywords

haptotaxisnonlinear diffusionECM remodellingglobal solution

MSC classification

Primary: 35M13: Initial-boundary value problems for equations of mixed type
Secondary: 35K65: Degenerate parabolic equations 92C17: Cell movement (chemotaxis, etc.)
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 32
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Byrne, H. M., Chaplain, M. A. J., J.Pettet, G. and Mcelwain, D. L. S.. Mathematical model of trophoblast invasion. J. Theor. Med. 1 (1999), 275–286.Google Scholar
Byrne, H. M., Chaplain, M. A. J., J.Pettet, G. and Mcelwain, D. L. S.. An analysis of a mathematical model of trophoblast invasion. Appl. Math. Lett. 14 (2001), 1005–1010.CrossRefGoogle Scholar
Chaplain, M. A. J. and Anderson, A. R. A., Mathematical modelling of tissue invasion, In: Preziosi, L., Ed., Cancer Modelling and Simulation (Chapman Hall/CRC, 2003), pp. 269–297.CrossRefGoogle Scholar
Chaplain, M. A. J. and Lolas, G.. Mathematical modelling of cancer invasion of tissue: dynamic heterogeneity. Netw. Heterogeneous Media 1 (2006), 399–439.CrossRefGoogle Scholar
Cao, X.. Boundedness in a three-dimensional chemotaxis-haptotaxis model. Z. Angew. Math. Phys. 67 (2016), 11.CrossRefGoogle Scholar
Hillen, T., Painter, K. J. and Winkler, M.. Convergence of a cancer invasion model to a logistic chemotaxis model. Math. Models Methods Appl. Sci. 25 (2013), 165–198.CrossRefGoogle Scholar
Jin, C.. Boundedness and global solvability to a chemotaxis-haptotaxis model with slow and fast diffusion. Discrete Contin. Dyn. Syst. Ser. B 23 (2018), 1675–1688.Google Scholar
Jin, C.. Global classical solutions and convergence to a mathematical model for cancer cells invasion and metastatic spread. J. Differ. Equ. 269 (2020), 3987–4021.CrossRefGoogle Scholar
Jin, C.. Global bounded weak solutions and asymptotic behavior to a chemotaxis-Stokes model with non-Newtonian filtration slow diffusion. J. Differ. Equ. 28 (2021), 148–184.CrossRefGoogle Scholar
Jin, C.. Global classical solution and boundedness to a chemotaxis-haptotaxis model with re-establishment mechanisms. Bull. Lond. Math. Soc. 50 (2018), 598–618.CrossRefGoogle Scholar
Jin, C.. Global strong solution and periodic dynamic behavior to Chaplain-Lolas model. J. Dyna. Diff. Eqns. (2022). doi:10.1007/s10884-022-10210-wGoogle Scholar
Li, Y. and Lankeit, J.. Boundedness in a chemotaxis–Chaptotaxis model with nonlinear diffusion. Nonlinearity 29 (2016), 1564–1595.CrossRefGoogle Scholar
Marciniak-Czochra, A. and Ptashnyk, M.. Boundedness of solutions of a haptotaxis model. Math. Models Methods Appl. Sci. 20 (), –.Google Scholar
Mizoguchi, N. and Souplet, P.. Nondegeneracy of blow-up points for the parabolic Keller-Segel system. Ann. I. H. Poincaré - AN 31 (2014), 851–875.Google Scholar
Pang, P. H. and Wang, Y.. Global existence of a two-dimensional chemotaxis-haptotaxis model with remodeling of non-diffusible attractant. J. Differ. Equ. 263 (2017), 1269–1292.CrossRefGoogle Scholar
Pang, P. H. and Wang, Y.. Global boundedness of solutions to a chemotaxis-haptotaxis model with tissue remodeling. Math. Models Methods Appl. Sci. 28 (2018), 2211–2235.CrossRefGoogle Scholar
Stinner, C. and Surulescu, C.. A multiscale model for pH-tactic invasion with time-varying carrying capacities. IMA J. Appl. Math. 80 (2015), 1300–1321.CrossRefGoogle Scholar
Tao, Y. and Wang, M.. Global solution for a chemotactic-haptotactic model of cancer invasion. Nonlinearity 21 (2008), 2221–2238.CrossRefGoogle Scholar
Tao, Y. and Winkler, M.. A chemotaxis-haptotaxis model: the roles of nonlinear diffusion and logistic source. SIAM J. Math. Anal. 43 (2011), 685–704.CrossRefGoogle Scholar
Tao, Y. and Winkler, M.. Large time behavior in a multidimensional chemotaxis-haptotaxis model with slow signal diffusion. SIAM J. Math. Anal. 47 (2015), 4229–4250.CrossRefGoogle Scholar
Wang, Y.. Boundedness in the higher-dimensional chemotaxis-haptotaxis model with nonlinear diffusion. J. Differ. Equ. 260 (2016), 1975–1989.CrossRefGoogle Scholar
Wang, Y. and Ke, Y.. Large time behavior of solution to a fully parabolic chemotaxis-haptotaxis model in higher dimensions. J. Differ. Equ. 260 (2016), 6960–6988.CrossRefGoogle Scholar
Walker, C. and Webb, G. F.. Global existence of classical solutions for a haptotaxis model. SIAM J. Math. Anal. 38 (2007), 1694–1713.CrossRefGoogle Scholar
Zheng, J.. Boundedness of solutions to a quasilinear higher-dimensional chemotaxis-haptotaxis model with nonlinear diffusion. Discrete Contin. Dyn. Syst. 37 (2017), 627–643.CrossRefGoogle Scholar