Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Morel, Jean Michel
1985.
Runge property and multiplicity of solutions for elliptic equations in ?N with a monotone nonlinearity.
Manuscripta Mathematica,
Vol. 54,
Issue. 1-2,
p.
165.
Goldstein, Jerome A.
and
Rieder, Gisèle Ruiz
1986.
Differential Equations in Banach Spaces.
Vol. 1223,
Issue. ,
p.
110.
Brezis, H.
and
Oswald, L.
1987.
Singular solutions for some semilinear elliptic equations.
Archive for Rational Mechanics and Analysis,
Vol. 99,
Issue. 3,
p.
249.
Goldstein, Jerome A.
and
Rieder, Gisèle Ruiz
1987.
Differential Equations and Mathematical Physics.
Vol. 1285,
Issue. ,
p.
143.
Brezis, H.
and
Oswald, L.
1989.
Analysis and Continuum Mechanics.
p.
615.
Bernis, Francisco
1989.
Elliptic and parabolic semilinear problems without conditions at infinity.
Archive for Rational Mechanics and Analysis,
Vol. 106,
Issue. 3,
p.
217.
Boccardo, L.
and
Gallouet, T.
1992.
Strongly nonlinear elliptic equations having natural growth terms and L1 data.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 19,
Issue. 6,
p.
573.
del Vecchio, T.
1995.
Nonlinear elliptic equations with measure data.
Potential Analysis,
Vol. 4,
Issue. 2,
p.
185.
Boccardo, Lucio
Gallouët, Thierry
and
Orsina, Luigi
1996.
Existence and uniqueness of entropy solutions for nonlinear elliptic equations with measure data.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 13,
Issue. 5,
p.
539.
Boccardo, Lucio
GallouËt, Thierry
and
Orsina, Luigi
1997.
Existence and nonexistence of solutions for some nonlinear elliptic equations.
Journal d'Analyse Mathématique,
Vol. 73,
Issue. 1,
p.
203.
BREZIS, HAÏM
and
SERFATY, SYLVIA
2002.
A VARIATIONAL FORMULATION FOR THE TWO-SIDED OBSTACLE PROBLEM WITH MEASURE DATA.
Communications in Contemporary Mathematics,
Vol. 04,
Issue. 02,
p.
357.
Fiorenza, Alberto
and
Prignet, Alain
2003.
Orlicz capacities and applications to some existence questions for elliptic pdes having measure data.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 9,
Issue. ,
p.
317.
Véron, Laurent
2004.
Vol. 1,
Issue. ,
p.
593.
Brezis, Haı¨m
and
Ponce, Augusto C.
2005.
Reduced measures on the boundary.
Journal of Functional Analysis,
Vol. 229,
Issue. 1,
p.
95.
Fiorenza, Alberto
2005.
Elliptic and Parabolic Problems.
Vol. 63,
Issue. ,
p.
259.
Gallouët, Thierry
2005.
Elliptic and Parabolic Problems.
Vol. 63,
Issue. ,
p.
279.
Kon'kov, A. A.
2006.
Behavior of Solutions of Quasilinear Elliptic Inequalities.
Journal of Mathematical Sciences,
Vol. 134,
Issue. 3,
p.
2073.
Chrif, M.
and
El Manouni, S.
2008.
On a strongly anisotropic equation withL1data.
Applicable Analysis,
Vol. 87,
Issue. 7,
p.
865.
Yao, Fengping
2009.
Optimal regularity for Schrödinger equations.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 71,
Issue. 11,
p.
5144.
Bendahmane, Mostafa
Chrif, Moussa
and
El Manouni, Said
2010.
Elliptic equations in weighted Sobolev spaces of infinite order with L
1
data.
Mathematical Methods in the Applied Sciences,
Vol. 33,
Issue. 1,
p.
49.
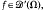 , in order that (P) has a solution. Roughly speaking, this condition is f = −ΔV + g, with g ∈ L1(Ω) and γ(., V) ∈ L1(Ω)
, in order that (P) has a solution. Roughly speaking, this condition is f = −ΔV + g, with g ∈ L1(Ω) and γ(., V) ∈ L1(Ω)

