Article contents
Regularity of the extremal solutions associated with elliptic systems
Published online by Cambridge University Press: 27 December 2018
Abstract
We examine the elliptic system given by
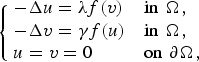 $$\left\{ {\matrix{ {-\Delta u = \lambda f(v)} \hfill & {{\rm in }\,\,\Omega ,} \hfill \cr {-\Delta v = \gamma f(u)} \hfill & {{\rm in }\,\,\Omega ,} \hfill \cr {u = v = 0} \hfill & {{\rm on }\,\,\partial \Omega ,} \hfill \cr } } \right.$$
$$\left\{ {\matrix{ {-\Delta u = \lambda f(v)} \hfill & {{\rm in }\,\,\Omega ,} \hfill \cr {-\Delta v = \gamma f(u)} \hfill & {{\rm in }\,\,\Omega ,} \hfill \cr {u = v = 0} \hfill & {{\rm on }\,\,\partial \Omega ,} \hfill \cr } } \right.$$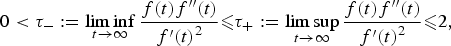 $$0 < \tau _-: = \mathop {\lim \inf }\limits_{t\to \infty } \displaystyle{{f(t){f}^{\prime \prime}(t)} \over {{f}^{\prime}{(t)}^2}} \les \tau _ + : = \mathop {\lim \sup }\limits_{t\to \infty } \displaystyle{{f(t){f}^{\prime \prime}(t)} \over {{f}^{\prime}{(t)}^2}} \les 2,$$
$$0 < \tau _-: = \mathop {\lim \inf }\limits_{t\to \infty } \displaystyle{{f(t){f}^{\prime \prime}(t)} \over {{f}^{\prime}{(t)}^2}} \les \tau _ + : = \mathop {\lim \sup }\limits_{t\to \infty } \displaystyle{{f(t){f}^{\prime \prime}(t)} \over {{f}^{\prime}{(t)}^2}} \les 2,$$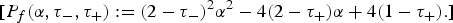 $$[P_{f}(\alpha,\tau_{-},\tau_{+}):=(2-\tau_{-})^{2} \alpha^{2}- 4(2-\tau_{+})\alpha+4(1-\tau_{+}).]$$
$$[P_{f}(\alpha,\tau_{-},\tau_{+}):=(2-\tau_{-})^{2} \alpha^{2}- 4(2-\tau_{+})\alpha+4(1-\tau_{+}).]$$
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 149 , Issue 4 , August 2019 , pp. 1037 - 1046
- Copyright
- Copyright © Royal Society of Edinburgh 2018
References
- 1
- Cited by


