Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T01:30:28.674Z Has data issue: false hasContentIssue false
  • English
  • Français

A reduction principle for topological classification of nonautonomous differential equations

Published online by Cambridge University Press:  14 November 2011

Nguyen Van Minh
Nguyen Van Minh
Affiliation:
Chair of Mathematical Methods in Control Theory, Department of Mathematics and Mechanics, Belorussian State University, Minsk 220 080, Belorussia
Get access Rights & Permissions [Opens in a new window]

Synopsis

The paper is concerned with equations of the form x' = A(t)x +f(t, x), where A is a continuous matrix function defined on ℝ, f is a continuous vector-valued function of (t, x) with f(t, 0) = 0. It is proved that if x' = A(t)x has an exponential trichotomy, A is bounded and f satisfies the Lipschitz condition with coefficient sufficiently small, then these equations are topologically equivalent to the systems of equations of the form 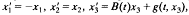, where B, g satisfy the same conditions as A, f.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 123 , Issue 4 , 1993 , pp. 621 - 632
Copyright
Copyright © Royal Society of Edinburgh 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Arnold, V. I.. Ordinary Differential Equations (Moscow: Nauka, 1975; in Russian).Google Scholar
2Aulbach, B.. Continuous and Discrete Dynamics near Manifolds of Equilibrium, Lecture Notes in Mathematics 1058 (Berlin: Springer, 1984).CrossRefGoogle Scholar
3Aulbach, B.. A reduction principle for nonautonomous differential equations. Arch. Math. 39 (1982), 217–232.CrossRefGoogle Scholar
4Bylov, B. F., Vinograd, R. E., Grobman, D. M. and Niemytski, V. V.. Theory of Lyapunov Exponents (Moscow: Nauka, 1966; in Russian).Google Scholar
5Coppel, W. A.. Dichotomies in Stability Theory, Lecture Notes in Mathematics 1629 (Berlin: Springer, 1978).CrossRefGoogle Scholar
6Daletski, Ju. L. and Krein, M. G.. Stability of Solutions of Differential Equations in Banach Space (Moscow: Nauka, 1970; in Russian).Google Scholar
7Kelley, A.. Stability of the center-stable manifold. J. Math. Anal. Appl. 18 (1967), 336–344.CrossRefGoogle Scholar
8Knobloch, H. W. and Kappel, F.. Gewohnliche Differentialgleichugen (Stuttgart: Teubner, 1974).CrossRefGoogle Scholar
9Minh, Nguyen Van. On a topological classification of nonautonomous differential equations. Colloq. Math. Soc. Janos Bolyai 53 (1988), 421–426.Google Scholar
10Palmer, K. J.. A characterization of exponential dichotomy in terms of topological equivalence. J. Math. Anal. Appl. 69 (1979), 8–16.CrossRefGoogle Scholar
11Pliss, V. A.. A reduction principle in theory of stability of motion. Izv. Akad. Nauk. SSSR ser. Mat 28 (1964), 1297–1324 (in Russian).Google Scholar
12Sacker, R. and Sell, G.. A spectral theory for linear differential systems. J. Differential Equations 27 (1978), 320–358.CrossRefGoogle Scholar
13Sell, G.. The structure of a flow in the vicinity of an almost periodic motion. J. Differential Equations 27 (1978), 359–393.CrossRefGoogle Scholar
14Tihonova, E. A.. Analogy and homeomorphism of perturbed and unperturbed systems with block-triangular matrix. Differentsialnye Uravneniya 7 (1970), 1221–1229 (in Russian).Google Scholar