Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T13:26:11.632Z Has data issue: false hasContentIssue false
  • English
  • Français

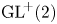A rank-one convex, nonpolyconvex isotropic function on $\textrm {GL}^{\!+}(2)$ with compact connected sublevel sets

Part of: Real functions Functions of several variables Elastic materials

Published online by Cambridge University Press:  02 February 2022

Jendrik Voss ,
Ionel-Dumitrel Ghiba ,
Robert J. Martin  and
Patrizio Neff
Jendrik Voss
Affiliation:
Chair for Nonlinear Analysis and Modeling, Faculty of Mathematics, University of Duisburg-Essen, Thea-Leymann-Str. 9, 45127, Essen, Germany ([email protected].)
Ionel-Dumitrel Ghiba
Affiliation:
Department of Mathematics, Alexandru Ioan Cuza University of Iaşi, Blvd. Carol I, no. 11, 700506, Iaşi, Romania, Octav Mayer Institute of Mathematics of the Romanian Academy, Iaşi Branch, 700505, Iaşi, Romania
Robert J. Martin
Affiliation:
Chair for Nonlinear Analysis and Modeling, Faculty of Mathematics, University of Duisburg-Essen, Thea-Leymann-Str. 9, 45127, Essen, Germany Institute for Technologies of Metal, University of Duisburg-Essen, Friedrich-Ebert-Str. 12, 47119, Duisburg, Germany
Patrizio Neff
Affiliation:
Chair for Nonlinear Analysis and Modeling, Faculty of Mathematics, University of Duisburg-Essen, Thea-Leymann-Str. 9, 45127, Essen, Germany
Get access Rights & Permissions [Opens in a new window]

Abstract

According to a 2002 theorem by Cardaliaguet and Tahraoui, an isotropic, compact and connected subset of the group 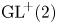$\textrm {GL}^{\!+}(2)$ of invertible 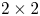$2\times 2$ - - matrices is rank-one convex if and only if it is polyconvex. In a 2005 Journal of Convex Analysis article by Alexander Mielke, it has been conjectured that the equivalence of rank-one convexity and polyconvexity holds for isotropic functions on 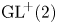$\textrm {GL}^{\!+}(2)$ as well, provided their sublevel sets satisfy the corresponding requirements. We negatively answer this conjecture by giving an explicit example of a function 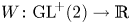$W\colon \textrm {GL}^{\!+}(2)\to \mathbb {R}$ which is not polyconvex, but rank-one convex as well as isotropic with compact and connected sublevel sets.

Keywords

quasiconvexityrank-one convexitypolyconvexitynonlinear elasticityhyperelasticityweak lower semi-continuityisotropic setscalculus of variations

MSC classification

Primary: 26B25: Convexity, generalizations
Secondary: 26A51: Convexity, generalizations 74B20: Nonlinear elasticity
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 2 , April 2022 , pp. 356 - 381
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alibert, J.-J. and Dacorogna, B.. An example of a quasiconvex function that is not polyconvex in two dimensions. Arch. Ration. Mech. Anal. 117 (1992), 155–166.CrossRefGoogle Scholar
Astala, K., Iwaniec, T. and Martin, G.. Elliptic Partial Differential Equations and Quasiconformal Mappings in the Plane (Princeton, NJ: Princeton University Press, 2008).CrossRefGoogle Scholar
Aubert, G.. On a counterexample of a rank 1 convex function which is not polyconvex in the case n= 2. Proc. R. Soc. Edinb. A, Math. 106 (1987), 237–240.CrossRefGoogle Scholar
Aubert, G.. Contribution aux problèmes du calcul des variations et application à l’élasticité non linéaire’. Thèse de doctorat d’état (Paris VI, 1986).Google Scholar
Ball, J. M.. Convexity conditions and existence theorems in nonlinear elasticity. Arch. Ration. Mech. Anal. 63 (1976), 337–403.CrossRefGoogle Scholar
Ball, J. M.. Some open problems in elasticity. In Geometry, Mechanics, and Dynamics (eds. Newton, P. Holmes, P. Weinstein, A.). pp. 3–59 (New York: Springer, 2002).CrossRefGoogle Scholar
Ball, J. and Murat, F.. $W^{1},\,p$-quasiconvexity and variational problems for multiple integrals. J. Funct. Anal. 58 (1984), 225–253.CrossRefGoogle Scholar
Ball, J. M.. Does rank-one convexity imply quasiconvexity?. In Metastability and Incompletely Posed Problems (eds. Antman, S. S. Ericksen, J. Kinderlehrer, D. Müller, I.), vol. 3, pp. 17–32 (New York: Springer, 1987).CrossRefGoogle Scholar
Cardaliaguet, P. and Tahraoui, R.. Sur l’équivalence de la 1-rang convexité et de la polyconvexité des ensembles isotropiques de $\mathbb {R}^{2}\times 2$. Comptes Rendus de l'Académie des Sci.-Ser. I-Math. 331 (2000), 851–856.Google Scholar
Cardaliaguet, P. and Tahraoui, R.. Equivalence between rank-one convexity and polyconvexity for isotropic sets of $\mathbb {R}^{2}\times 2$ (Part I). Nonlinear Anal. Theory Methods Appl. 50 (2002), 1201–1239.CrossRefGoogle Scholar
Cardaliaguet, P. and Tahraoui, R.. Equivalence between rank-one convexity and polyconvexity for isotropic sets of $\mathbb {R}^{2}\times 2$ (Part II). Nonlinear Anal. Theory Methods Appl. 50 (2002), 1179–1199.CrossRefGoogle Scholar
Chełmiński, K. and Kałamajska, A.. New convexity conditions in the calculus of variations and compensated compactness theory. ESAIM: Control, Optimisation Calc. Var. 12 (2006), 64–92.Google Scholar
Conti, S., Faraco, D., Maggi, F. and Müller, S.. Rank-one convex functions on 2$\times$2 symmetric matrices and laminates on rank-three lines. Calc. Var. Partial Differ. Equ. 24 (2005), 479–493.CrossRefGoogle Scholar
Conti, S., Lellis, C. D., Müller, S. and Romeo, M.. Polyconvexity equals rank-one convexity for connected isotropic sets in $M^{2}\times 2$. Comptes Rendus Math. 337 (2003), 233–238.CrossRefGoogle Scholar
Crouzeix, J.-P. and Ferland, J. A.. Criteria for quasi-convexity and pseudo-convexity: relationships and comparisons. Math. Program. 23 (1982), 193–205.CrossRefGoogle Scholar
Dacorogna, B.. Direct Methods in the Calculus of Variations, 2nd edn, vol. 78. Applied Mathematical Sciences (Berlin: Springer, 2008).Google Scholar
Dacorogna, B. and Marcellini, P.. A counterexample in the vectorial calculus of variations. In Material Instabilities in Continuum Mechanics (ed. Ball, J. M.), pp. 77–83 (Oxford: Oxford Science Publications, 1988).Google Scholar
Faraco, D., Székelyhidi, L.. Tartar's conjecture and localization of the quasiconvex hull in $\mathbb {R}^{2}\times 2$. Acta Math. 200 (2008), 279–305.CrossRefGoogle Scholar
Ghiba, I.-D., Martin, R. J. and Neff, P.. Rank-one convexity implies polyconvexity in isotropic planar incompressible elasticity. J. de Math. Pures et Appl. 116 (2018), 88–104.CrossRefGoogle Scholar
Grabovsky, Y.. From microstructure-independent formulas for composite materials to rank-one convex, non-quasiconvex functions. Arch. Ration. Mech. Anal. 227 (2018), 607–636.CrossRefGoogle Scholar
Harris, T. L., Kirchheim, B. and Lin, C.-C.. Two-by-two upper triangular matrices and Morrey's conjecture. Calc. Var. Partial Differ. Equ. 57 (2018), 1–12.CrossRefGoogle Scholar
Heinz, S.. Quasiconvexity equals lamination convexity for isotropic sets of $2\times 2$ matrices. Adv. Calc. Var. 8 (2015), 43–53.CrossRefGoogle Scholar
Knowles, J. K. and Sternberg, E.. On the failure of ellipticity of the equations for finite elastostatic plane strain. Arch. Ration. Mech. Anal. 63 (1976), 321–336.CrossRefGoogle Scholar
Knowles, J. K. and Sternberg, E.. On the failure of ellipticity and the emergence of discontinuous deformation gradients in plane finite elastostatics. J. Elast. 8 (1978), 329–379.CrossRefGoogle Scholar
Martin, R. J., Ghiba, I.-D. and Neff, P.. Rank-one convexity implies polyconvexity for isotropic, objective and isochoric elastic energies in the two-dimensional case’. Proc. R. Soc. Edinb. A 147A (2017), 571–597, available at arXiv:1507.00266.CrossRefGoogle Scholar
Martin, R. J., Voss, J., Ghiba, I.-D. and Neff, P.. Quasiconvex relaxation of isotropic functions in incompressible planar hyperelasticity. Proc. R. Soc. Edinb. A, Math. 150 (2020), 2620–2631.CrossRefGoogle Scholar
Martin, R. J., Voss, J., Ghiba, I.-D., Sander, O. and Neff, P.. The quasiconvex envelope of conformally invariant planar energy functions in isotropic hyperelasticity. J. Nonlinear Sci. 30 (2020), 2885–2923.CrossRefGoogle Scholar
Mielke, A.. Necessary and sufficient conditions for polyconvexity of isotropic functions. J. Convex Anal. 12 (2005), 291.Google Scholar
Mielke, A.. Personal communication at the GAMM annual meeting, Vienna, 2019.Google Scholar
Mirsky, L.. Symmetric gauge functions and unitarily invariant norms. Q. J. Math. 11 (1960), 50–59.CrossRefGoogle Scholar
Morrey, C. B.. Quasi-convexity and the lower semicontinuity of multiple integrals. Pac. J. Math. 2 (1952), 25–53.CrossRefGoogle Scholar
Müller, S.. Rank-one convexity implies quasiconvexity on diagonal matrices. Int. Math. Res. Not. 1999 (1999), 1087–1095.CrossRefGoogle Scholar
Parry, G. and Šilhavỳ, M.. On rank one connectedness, for planar objective functions. J. Elast. 58 (2000), 177–189.CrossRefGoogle Scholar
Parry, G.. On the planar rank-one convexity condition. Proc. R. Soc. Edinb. A, Math. 125 (1995), 247–264.CrossRefGoogle Scholar
Pedregal, P. and Šverák, V.. A note on quasiconvexity and rank-one convexity for $2 \times 2$ matrices. J. Convex Anal. 5 (1998), 107–118.Google Scholar
Rindler, F.. Calculus of Variations (Cham, Switzerland: Springer, 2018).CrossRefGoogle Scholar
Rosakis, P. and Simpson, H. C.. On the relation between polyconvexity and rank-one convexity in nonlinear elasticity. J. Elast. 37 (1994), 113–137.CrossRefGoogle Scholar
Schröder, J. and Neff, P.. Poly-, Quasi-and Rank-one Convexity in Applied Mechanics (Vienna: Springer Science & Business Media, 2010). doi: 10.1007/978-3-7091-0174-2.CrossRefGoogle Scholar
Sebestyén, G. and Székelyhidi, L. Jr. Laminates supported on cubes. J. Convex Anal. 24 (2017), 1217–1237.Google Scholar
Šilhavý, M.. An $\textrm {O}(n)$ invariant rank $1$ convex function that is not polyconvex. Theor. Appl. Mech. 28 (2002), 325–336.CrossRefGoogle Scholar
Šilhavỳ, M.. Convexity conditions for rotationally invariant functions in two dimensions. In Applied Nonlinear Analysis (eds. Sequeira, A. da Veiga, H. B. Videman, J. H.). pp. 513–530 (Boston: Springer, 2002).CrossRefGoogle Scholar
Šverák, V.. Rank-one convexity does not imply quasiconvexity. Proc. R. Soc. Edinb. A, Math. 120 (1992), 185–189.CrossRefGoogle Scholar
Székelyhidi, L. Jr. On the local structure of rank-one convex hulls. Proc. Am. Math. Soc. 134 (2006), 1963–1972.CrossRefGoogle Scholar
Voss, J., Ghiba, I.-D., Martin, R. J. and Neff, P.. Sharp rank-one convexity conditions in planar isotropic elasticity for the additive volumetric-isochoric split. J. Elast. 143 (2021), 301–335.CrossRefGoogle Scholar