Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T02:16:27.574Z Has data issue: false hasContentIssue false
  • English
  • Français

Pull-back attractors for three-dimensional Navier—Stokes—Voigt equations in some unbounded domains

Published online by Cambridge University Press:  30 May 2013

Cung The Anh  and
Pham Thi Trang
Cung The Anh
Affiliation:
Department of Mathematics, Hanoi National University of Education, 136 Xuan Thuy, Cau Giay, Hanoi, Vietnam ([email protected]; [email protected])
Pham Thi Trang
Affiliation:
Department of Mathematics, Hanoi National University of Education, 136 Xuan Thuy, Cau Giay, Hanoi, Vietnam ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

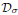We study the first initial–boundary-value problem for the three-dimensional non-autonomous Navier–Stokes–Voigt equations in an arbitrary (bounded or unbounded) domain satisfying the Poincaré inequality. The existence of a weak solution to the problem is proved by using the Faedo–Galerkin method. We then show the existence of a unique minimal finite-dimensional pull-back -attractor for the process associated with the problem, with respect to a large class of non-autonomous forcing terms. We also discuss relationships between the pull-back attractor, the uniform attractor and the global attractor.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 143 , Issue 2 , April 2013 , pp. 223 - 251
Copyright
Copyright © Royal Society of Edinburgh 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)