Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ruf, Bernhard
1994.
Borderline problems in the Calculus of Variations.
Rendiconti del Seminario Matematico e Fisico di Milano,
Vol. 64,
Issue. 1,
p.
159.
de Figueiredo, D. G.
Miyagaki, O. H.
and
Ruf, B.
1995.
Elliptic equations in R2 with nonlinearities in the critical growth range.
Calculus of Variations and Partial Differential Equations,
Vol. 3,
Issue. 2,
p.
139.
De Figueiredo, D. G.
and
Ruf, B.
1995.
Existence and non‐existence of radial solutions for elliptic equations with critical exponent in ℝ2.
Communications on Pure and Applied Mathematics,
Vol. 48,
Issue. 6,
p.
639.
de Figueiredo, D. G.
Miyagaki, O. H.
and
Ruf, B.
1995.
Djairo G. de Figueiredo - Selected Papers.
p.
423.
Dimurthi, A
and
Prashanth, S
1997.
Failure of Plais-Smale condition and blow-up analysis for the critical exponent problem inR 2.
Proceedings Mathematical Sciences,
Vol. 107,
Issue. 3,
p.
283.
Adimurthi
and
Struwe, Michael
2000.
Global Compactness Properties of Semilinear Elliptic Equations with Critical Exponential Growth.
Journal of Functional Analysis,
Vol. 175,
Issue. 1,
p.
125.
del Pino, Manuel
Musso, Monica
and
Ruf, Bernhard
2010.
New solutions for Trudinger–Moser critical equations in R2.
Journal of Functional Analysis,
Vol. 258,
Issue. 2,
p.
421.
de Souza, Manassés
2011.
On a singular class of elliptic systems involving critical growth in.
Nonlinear Analysis: Real World Applications,
Vol. 12,
Issue. 2,
p.
1072.
de Souza, Manassés
and
do Ó, João Marcos
2011.
On a singular and nonhomogeneous N-Laplacian equation involving critical growth.
Journal of Mathematical Analysis and Applications,
Vol. 380,
Issue. 1,
p.
241.
Lam, Nguyen
and
Lu, Guozhen
2012.
Sharp Adams type inequalities in Sobolev spaces Wm,nm(Rn) for arbitrary integer m.
Journal of Differential Equations,
Vol. 253,
Issue. 4,
p.
1143.
del Pino, Manuel
Musso, Monica
and
Ruf, Bernhard
2012.
Beyond the Trudinger-Moser supremum.
Calculus of Variations and Partial Differential Equations,
Vol. 44,
Issue. 3-4,
p.
543.
Yang, Yunyan
2012.
Adams type inequalities and related elliptic partial differential equations in dimension four.
Journal of Differential Equations,
Vol. 252,
Issue. 3,
p.
2266.
Figueroa, Pablo
and
Musso, Monica
2018.
Bubbling solutions for Moser–Trudinger type equations on compact Riemann surfaces.
Journal of Functional Analysis,
Vol. 275,
Issue. 10,
p.
2684.
Monari Soares, Sergio H.
and
Santaria Leuyacc, Yony R.
2019.
Singular Hamiltonian elliptic systems with critical exponential growth in dimension two.
Mathematische Nachrichten,
Vol. 292,
Issue. 1,
p.
137.
Deng, Shengbing
and
Tian, Xingliang
2022.
On a nonhomogeneous Kirchhoff type elliptic system with the singular Trudinger-Moser growth.
Discrete and Continuous Dynamical Systems,
Vol. 42,
Issue. 10,
p.
4761.
Santaria Leuyacc, Yony Raúl
2023.
A nonhomogeneous Schrödinger equation involving nonlinearity with exponential critical growth and potential which can vanish at infinity.
Results in Applied Mathematics,
Vol. 17,
Issue. ,
p.
100348.


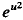 growth and for which
growth and for which
