Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-30T23:24:10.762Z Has data issue: false hasContentIssue false
  • English
  • Français

Oscillations in a dynamical model of phase transitions

Published online by Cambridge University Press:  11 July 2007

Deborah Brandon ,
Irene Fonseca  and
Pieter Swart
Deborah Brandon
Affiliation:
Department of Mathematical Sciences, Carnegie Mellon University, Pittsburgh, PA 15213, USA
Irene Fonseca
Affiliation:
Department of Mathematical Sciences, Carnegie Mellon University, Pittsburgh, PA 15213, USA
Pieter Swart
Affiliation:
Theoretical Division, Los Alamos National Laboratory, Los Alamos, NM 87545, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

The creation and propagation of oscillations in a model for the dynamics of fine structure under viscoelastic damping 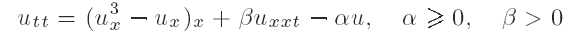is studied. It is shown that oscillations in the velocity ut are lost immediately as time evolves, while oscillations in the initial strain ux cannot be created, and they persist for all time if initially present. Uniqueness of generalized solutions (Young measures) is obtained, and a characterization of these Young measures is provided in the case of periodic modulated initial data.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 131 , Issue 1 , February 2001 , pp. 59 - 81
Copyright
Copyright © Royal Society of Edinburgh 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)