Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T01:50:18.440Z Has data issue: false hasContentIssue false
  • English
  • Français

Orbital compactness and asymptotic behaviour of nonlinear parabolic systems with functionals

Published online by Cambridge University Press:  14 November 2011

Reinhard Redlinger
Reinhard Redlinger
Affiliation:
Mathematics Research Center, University of Wisconsin–Madison, 610 Walnut Street, Madison, 53705, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Synopsis

Weakly coupled semilinear parabolic systems of the form 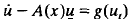with homogeneous boundary conditions are studied. The nonlinear function g: C([−r, 0] × Ω ℝn) → ℝn is assumed to be locally Lipschitz continuous with r≧0 a given real number and Ω ⊂ ℝm a bounded domain, 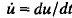, ut for t ≧ 0 is denned by ut (σ, ξ) = u(t + σ, ξ), − r ≦σ ≦ 0 ξ ∊Ω and A is a uniformly elliptic second order diagonal operator. Let u be a bounded classical solution. We first establish precompactness results for the orbit of u in several function spaces. Using these results and assuming that a Liapunov function V is known for the corresponding ordinary functional differential equation ż =g(zt), we then show under some general conditions that the limit set ω+ (as t→∞) of u consists of spatially homogeneous functions only. Moreover, ω+ is invariant with respect to z = g(z,) and V = 0 on ω+. The proof uses a Liapunov function for the full system whichis obtained from V via a simple construction (cf. (3.3)). The theory is illustrated with an example.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 105 , Issue 1 , 1987 , pp. 83 - 99
Copyright
Copyright © Royal Society of Edinburgh 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Brezis, H. and Friedman, A.. Nonlinear parabolic equations involving measures as initial conditions. J. Math. Pures Appl. 62 (1983), 73–97.Google Scholar
2Friedman, A.. Partial differential equations (New York, Holt, Rinehart and Winston, 1969).Google Scholar
3Hale, J.. Functional differential equations. Applied Mathematical Sciences 3 (New York, Springer-Verlag, 1971).Google Scholar
4Henry, D.. Geometric theory of semilinear parabolic equations. Lecture Notes in Mathematics 840 (Berlin: Springer-Verlag, 1981).Google Scholar
5Ladyzhenskaja, O. A., Solonnikov, V. A. and Ural'tseva, N. N.. Linear andquasilinear equations of parabolic type. Trans. Math. Monographs 23 (Providence, RI: American Mathematical Society, 1968).Google Scholar
6Ladyzhenskaja, O. A. and Ural'tseva, N. N.. Linear and quasilinear elliptic equations (New York: Academic Press, 1968).Google Scholar
7Mottoni, P. de, Orlandi, E. and Tesei, A.. Asymptotic behaviour for a system describing epidemics with migration and spatial spread of infection. Nonlinear Anal. 3 (1979), 663–675.CrossRefGoogle Scholar
8Redheffer, R. and Walter, W.. On parabolic systems of the Volterra prey-predator type. Nonlinear Anal. 7 (1983), 333–347.CrossRefGoogle Scholar
9Redheffer, R., Redlinger, R. and Walter, W.. A theory of LaSalle–Liapunov type for parabolic systems (unpublished).Google Scholar
10Redlinger, R.. Über die C 2-Kompaktheit der Bahn von Lösungen semilinearer parabolischer Systeme. Proc. Roy. Soc. Edinburgh Sect A 93 (1982), 99–103.CrossRefGoogle Scholar
11Redlinger, R.. Existence theorems for semilinear parabolic systems with functional. Nonlinear Anal. 8 (1984), 667–682.CrossRefGoogle Scholar
12Rothe, F.. Global solutions of reaction-diffusion systems. Lecture Notes in Mathematics 1072 (Berlin: Springer-Verlag, 1984).Google Scholar
13Sobolevskij, P. E.. Equations of parabolic type in a Banach space. Amer. Math. Soc. Transl. (2) 49 (1966), 1–62.Google Scholar
14Stewart, H. B.. Generation of analytic semigroups by strongly elliptic operators. Trans. Amer. Math. Soc. 199 (1974), 141–162.CrossRefGoogle Scholar
15Stewart, H. B., Generation of analytic semigroups by strongly elliptic operators under general boundary conditions. Trans. Amer. Math. Soc. 259 (1980), 299–310.CrossRefGoogle Scholar
16Travis, C. C. and Webb, G. F.. Existence and stability for partial differential equations. Trans. Amer. Math. Soc. 200 (1974), 395–418.CrossRefGoogle Scholar
17Travis, C. C. and Webb, G. F.. Partial differential equations with deviating arguments inthe time variable. J. Math. Anal. Appl. 56 (1976), 397–409.CrossRefGoogle Scholar