Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T02:06:28.513Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal existence and uniqueness in a nonlinear diffusion–absorption equation with critical exponents

Published online by Cambridge University Press:  14 November 2011

M. Chaves ,
J. L. Vazquez  and
M. Walias
M. Chaves
Affiliation:
Departamento de Matemáticas, Universidad Autónoma de Madrid, 28049 Madrid, Spain
J. L. Vazquez
Affiliation:
Departamento de Matemáticas, Universidad Autónoma de Madrid, 28049 Madrid, Spain
M. Walias
Affiliation:
Departamento de Matemáticas, Universidad Autónoma de Madrid, 28049 Madrid, Spain
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the existence and uniqueness of non-negative solutions of the nonlinear parabolic equation

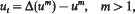
posed in Q = RN × (0, ∞) with general initial data u(x, 0) = u0(x) ≧ 0. We find optimal exponential growth conditions for existence of solutions. Similar conditions apply for uniqueness, but the growth rate is different. Such conditions strongly depart from the linear case m = 1, ut = Δu – u, and also from the purely diffusive case ut = Δum.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 127 , Issue 2 , 1997 , pp. 217 - 242
Copyright
Copyright © Royal Society of Edinburgh 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Aronson, D. G. and Caffarelli, L. A.. The initial trace of a solution of the porous medium equation. Tram. Amer. Math. Soc. 280 (1983), 351–661.CrossRefGoogle Scholar
2Bènilan, Ph., Crandall, M. G. and Pierre, M.. Solutions of the PME in RN with optimal conditions on the initial data. Indiana Univ. Math. J. 33 (1984), 51–87.CrossRefGoogle Scholar
3Bertsch, M., Kersner, R. and Peletier, L. A.. Sur le comportement de la frontiere libre dans une équation en théorie de la filtration. C. R. Acad. Sci. Paris Sér. 1 Math. 295 (1982), 63–6.Google Scholar
4Bertsch, M., Nanbu, T. and Peletier, L. A.. Decay of solutions of degenerate nonlinear diffusion equation. Nonlinear Anal. 6 (1982), 539–54.CrossRefGoogle Scholar
5Carr, J.. Applications of Centre Manifold Theory, Applied Mathematical Sciences 35 (Berlin: Springer, 1981).CrossRefGoogle Scholar
6Chaves, M. and Vázquez, J. L. Non-uniqueness in nonlinear heat propagation: A heat wave coming from infinity. J. Differential Integral Equations 9 (1996), 21–50.Google Scholar
7Dahlberg, B. E. J. and Kenig, C. E.. Non-negative solutions of the porous medium equation. Comm. Partial Differential Equations 9 (1984), 409–37.CrossRefGoogle Scholar
8Guckenheimer, J. and Holmes, P.. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields (Berlin: Springer, 1983).CrossRefGoogle Scholar
9Kalashnikov, A. S.. The effect of absorption on heat propagation in a medium in which thermal conductivity depends on temperature. Zh. Vychisl. Mat. Mat. Fiz. 16 (1976), 689–96 (in Russian).Google Scholar
10Kalashnikov, A. S.. Some questions of the qualitative theory of nonlinear degenerate parabolic second-order equations. Uspekhi Mat. Nauk 42 (1987), 135–76 (in Russian).Google Scholar
11Kamin, S., Peletier, L. A. and Vázquez, J. L.. A nonlinear diffusion–absorption equation with unbounded data. In ‘Nonlinear Diffusion Equations and their Equilibrium States, 3’, volume 7 in the series Progress in Nonlinear Diff. Eqns. and Appl. 243–63 (Boston: Birkhäuser Verlag, 1992).Google Scholar
12Kamin, S., Peletier, L. A. and Vázquez, J. L.. Classification of singular solutions of a nonlinear heat equation. Duke Math. J. 58 (1989), 601–15.CrossRefGoogle Scholar
13Kersner, R.. Degenerate parabolic equations with general nonlinearities. Nonlinear Anal. 4 (1980), 1043–62.CrossRefGoogle Scholar
14Ladyzhenskaya, O. A., Solonnikov, V. A. and Ural'tseva, N. N.. Linear and quasilinear equations of parabolic type. Translations of Mathematical Monographs 23 (Providence, RI: American Mathematical Society, 1968).Google Scholar
15McLeod, B., Peletier, L. A. and Vázquez, J. L.. Solutions of a nonlinear ODE appearing in the theory of diffusion with adsorption. Differential Integral Equations 4 (1991), 1–14.CrossRefGoogle Scholar
16Peletier, L. A.. Nonlinear diffusion equations with unbounded initial data. In Seminario de Matemdtica Aplicada, Universidad Complutense de Madrid, 1991, 1–12.Google Scholar
17Tikhonov, A. N.. Théorèmes d'unicite pour l'equation de la chaleur. Mat. Sb. 42 (1935), 199–216.Google Scholar
18Vázquez, J. L.. Comportamiento asintotico de las ecuaciones parabólicas no lineales. In III Congreso de Matemdtica Aplicada, XIII CEDYA, Madrid 1993, 38–58, Casal, A. et al. eds, 1995 (in Spanish).Google Scholar
19Vazquez, J. L. and Walias, M.. Existence and uniqueness of solutions of diffusion–absorption equation with general data. J. Differential Integral Equations 7 (1994), 15–36.Google Scholar
20Widder, D. V.. The Heat Equation (New York: Academic Press, 1975).Google Scholar