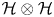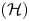Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yang, Zhiyuan
2024.
A Conjugate System for Twisted Araki–Woods von Neumann Algebras of Finite Dimensional Spaces.
International Mathematics Research Notices,
Vol. 2024,
Issue. 17,
p.
12044.