Article contents
On the swirling flow between rotating coaxial disks, asymptotic behaviour, II
Published online by Cambridge University Press: 14 November 2011
Synopsis
Consider solutions 〈H(x, ε), G(x, ε)〉 of the von Kármán equations for the swirling flow between two rotating coaxial disks
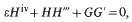
and
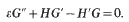
We assume that |H(x, ε)| + |Hʹ(x, ε)| + |G(x, ε)|≦B. This work considers shapes and asymptotic behaviour as ε→0+. We consider the type of limit functions 〈H(x), G(x)〉 that are permissible. In particular, if 〈H(x, ε), G(x, ε)〉 also satisfy the boundary conditions H(0, ε)=H(1, ε)=0, Hʹ(0, ε)=Hʹ(1, ε)=0 then H(x) has no simple zeros. That is, there does not exist a point Z ε [0, 1] such that H(x)=0, Hʹ(z)≠0. Moreover, the case of “cells” which oscillate is studied in detail.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 90 , Issue 3-4 , 1981 , pp. 317 - 346
- Copyright
- Copyright © Royal Society of Edinburgh 1981
References
- 1
- Cited by


