Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-12T22:24:35.679Z Has data issue: false hasContentIssue false
  • English
  • Français

On the relation between distinct particular solutions of equation

Published online by Cambridge University Press:  14 November 2011

Guan Ke-ying  and
W. N. Everitt
Guan Ke-ying
Affiliation:
Department of Mathematics, The University of Birmingham, Birmingham BT15 2TT, U.K.
W. N. Everitt
Affiliation:
Department of Mathematics, The University of Birmingham, Birmingham BT15 2TT, U.K.
Get access Rights & Permissions [Opens in a new window]

Synopsis

There exists a relation (1.5) between any n + 2 distinct particular solutions of the differential equation

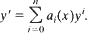
In this paper, we show that when and only when n = 0, 1 and 2, this relation can be represented by the following form:

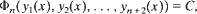
provided the form of this relation function Φn depends only on n and is independent of the coefficients of the equation. This result reveals interesting properties of these non-linear differential equations.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 123 , Issue 5 , 1993 , pp. 917 - 926
Copyright
Copyright © Royal Society of Edinburgh 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Arnold, V. I.. Ordinary Differential Equations (Massachusetts: MIT Press, 1973).Google Scholar
2Mirsky, L.. An Introduction to Linear Algebra (Oxford: Clarendon Press, 1955).Google Scholar
3Petrovski, J. G.. Ordinary Differential Equations (Englewood Cliffs, N.J.: Prentice-Hall, 1966).Google Scholar
4Hille, E.. Ordinary Differential Equations in the Complex Domain (New York: John Wiley & Sons, 1976).Google Scholar
5Baxandall, P. and Liebeck, H.. Vector Calculus (Oxford: Clarendon Press, 1986).Google Scholar
6, Qin Yuanxun. Theory and practice of approximate analytic solutions of ordinary differential equations. Appl. Comp. Appl. Math. 6 (1978), 35–54.Google Scholar