On the open problems connected to the results of Lazer and Solimini
Published online by Cambridge University Press: 30 January 2014
Abstract
A well-known theorem proved by Lazer and Solimini claims that the singular equation
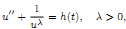
has a periodic solution if and only if the mean value of the continuous external force is positive. In this paper, we show that this result cannot be extended to the case when h is an integrable function, unless additional assumptions are introduced. In addition, for each p ≥ 1 and h-integrable function in the pth power, we give a sharp condition guaranteeing the existence of periodic solutions to the above-mentioned equation, showing that there is a close relation between p and the order of the singularity λ.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 144 , Issue 1 , February 2014 , pp. 109 - 118
- Copyright
- Copyright © Royal Society of Edinburgh 2014
- 8
- Cited by


