Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T10:59:48.389Z Has data issue: false hasContentIssue false
  • English
  • Français

On the initial value problem for a class of nonlinear biharmonic equation with time-fractional derivative

Part of: Partial differential equations Parabolic equations and systems Real functions Other special functions

Published online by Cambridge University Press:  26 August 2021

Anh Tuan Nguyen Open the ORCID record for Anh Tuan Nguyen [Opens in a new window] ,
Tomás Caraballo  and
Nguyen Huy Tuan
Anh Tuan Nguyen
Affiliation:
Division of Applied Mathematics, Thu Dau Mot University, Binh Duong Province, Vietnam ([email protected])
Tomás Caraballo
Affiliation:
Departamento de Ecuaciones Diferenciales y Análisis Numérico C/ Tarfia s/n, Facultad de Matemáticas, Universidad de Sevilla, Sevilla 41080, Spain ([email protected])
Nguyen Huy Tuan
Affiliation:
Department of Mathematics and Computer Science, University of Science, Ho Chi Minh City, Vietnam Vietnam National University, Ho Chi Minh City, Vietnam ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this study, we investigate the intial value problem (IVP) for a time-fractional fourth-order equation with nonlinear source terms. More specifically, we consider the time-fractional biharmonic with exponential nonlinearity and the time-fractional Cahn–Hilliard equation. By using the Fourier transform concept, the generalized formula for the mild solution as well as the smoothing effects of resolvent operators are proved. 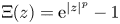For the IVP associated with the first one, by using the Orlicz space with the function $\Xi (z)={\textrm {e}}^{|z|^{p}}-1$ and some embeddings between it and the usual Lebesgue spaces, we prove that the solution is a global-in-time solution or it shall blow up in a finite time if the initial value is regular. In the case of singular initial data, the local-in-time/global-in-time existence and uniqueness are derived. Also, the regularity of the mild solution is investigated. For the IVP associated with the second one, some modifications to the generalized formula are made to deal with the nonlinear term. We also establish some important estimates for the derivatives of resolvent operators, they are the basis for using the Picard sequence to prove the local-in-time existence of the solution.

Keywords

Biharmonic equationsCahn–Hilliard equationsexponential nonlinearityfourth orderglobal existencelocal existencetime-fractionalwell-posedness

MSC classification

Primary: 26A33: Fractional derivatives and integrals
Secondary: 33E12: Mittag-Leffler functions and generalizations 35B40: Asymptotic behavior of solutions 35K30: Initial value problems for higher-order parabolic equations 35K58: Semilinear parabolic equations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 4 , August 2022 , pp. 989 - 1031
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abels, H., Bosia, S. and Grasselli, M.. Cahn–Hilliard equation with nonlocal singular free energies. Ann. Mat. Pura Appl. 194 (2015), 1071–1106.CrossRefGoogle Scholar
Akagi, G., Schimperna, G. and Segatti, A.. Fractional Cahn–Hilliard, Allen–Cahn and porous medium equations. J. Diff. Equ. 261 (2016), 2935–2985.CrossRefGoogle Scholar
Andrade, B. and Viana, A.. Abstract Volterra integrodifferential equations with applications to parabolic models with memory. Math. Ann. 369 (2017), 1131–1175.CrossRefGoogle Scholar
De Andrade, B. and Viana, A.. On a fractional reaction-diffusion equation. Z. Angew. Math. Phys. 68 (2017), 59.CrossRefGoogle Scholar
Asogwa, S. A., Mijena, J. B. and Nane, E.. Blow-up results for space-time fractional stochastic partial differential equations. Potential Anal. 53 (2020), 357–386.CrossRefGoogle Scholar
Bartolucci, D., Leoni, F., Orsina, L. and Ponce, A. C.. Semilinear equations with exponential nonlinearity and measure data. Ann. Inst. H. Poincaré Anal. Non Linéaire 22 (2005), 799–815.Google Scholar
Bebernes, J. and Eberly, D.. Mathematical problems from combustion theory. Applied Mathematical Sciences, vol. 83 (New York: Springer-Verlag, 1989).CrossRefGoogle Scholar
Blowey, J. and Elliott, C.. The Cahn–Hilliard gradient theory for phase separation with non smooth free energy I. Mathematical analysis. Eur. J. Appl. Math. 2 (1992), 147–179.CrossRefGoogle Scholar
Bosch, J. and Stoll, M.. A fractional inpainting model based on the vector-valued Cahn–Hilliard equation. SIAM J. Imaging Sci. 8 (2015), 2352–2382.CrossRefGoogle Scholar
Caffarelli, L. A. and Muler, N. E.. An $L^{\infty }$ bound for solutions of the Cahn–Hilliard equation. Arch. Rational Mech. Anal. 133 (1995), 129–144.CrossRefGoogle Scholar
Cahn, J. W. and Hilliard, J. E.. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 28 (1958), 258–267.CrossRefGoogle Scholar
Caputo, M.. Linear models of dissipation whose $Q$ is almost frequency independent. II. Fract. Calc. Appl. Anal. 11 (2008), 4–14. Reprinted from Geophys. J. R. Astr. Soc. 13 (1967), 529–539.Google Scholar
de Carvalho-Neto, P. M. and Planas, G.. Mild solutions to the time fractional Navier–Stokes equations in ${\mathbb {R}}^{N}$. J. Diff. Equ. 259 (2015), 2948–2980.CrossRefGoogle Scholar
Chen, Y., Gao, H., Garrido-Atienza, M. and Schmalfuß, B.. Pathwise solutions of SPDEs driven by Hölder - continuous integrators with exponent larger than 1/2 and random dynamical systems. Discrete Contin. Dyn. Syst. – Ser. A 34 (2014), 79–98.CrossRefGoogle Scholar
Cherfils, L., Miranville, A. and Zelik, S.. On a generalized Cahn–Hilliard equation with biological applications. Discrete Contin. Dyn. Syst – Ser. B. 19 (2014), 2013–2026.Google Scholar
Dinh, V. D., Keraani, S. and Majdoub, M.. Long time dynamics for the focusing nonlinear Schrödinger equation with exponential nonlinearities. Dyn. Partial Diff. Equ. 17 (2020), 329–360.CrossRefGoogle Scholar
Dipierro, S., Valdinoci, E. and Vespri, V.. Decay estimates for evolutionary equations with fractional time-diffusion. J. Evol. Equ. 19 (2019), 435–462.CrossRefGoogle Scholar
Dipierro, S., Pellacci, B., Valdinoci, E. and G. Verzini, E.. Time-fractional equations with reaction terms: fundamental solutions and asymptotics. Discrete Contin. Dyn. Syst. 41 (2021), 257–275.CrossRefGoogle Scholar
Dlotko, T.. Global attractor for the Cahn–Hilliard equation in $H^{2}$ and $H^{3}$. J. Diff. Equ. 113 (1994), 381–393.CrossRefGoogle Scholar
Dong, H. and Kim, D.. $L_p$-estimates for time fractional parabolic equations with coefficients measurable in time. Adv. Math. 345 (2019), 289–345.CrossRefGoogle Scholar
Dong, H. and Kim, D.. $L_p$-estimates for time fractional parabolic equations in divergence form with measurable coefficients. J. Funct. Anal. 278 (2020), 108338, 66 pp.CrossRefGoogle Scholar
Furioli, G., Kawakami, T., Ruf, B. and Terraneo, E.. Asymptotic behavior and decay estimates of the solutions for a nonlinear parabolic equation with exponential nonlinearity. J. Diff. Equ. 262 (2017), 145–180.CrossRefGoogle Scholar
Galaktionov, V. A. and Pohozaev, S. I.. Existence and blow-up for higher-order semilinear parabolic equations: Majorizing order-preserving operators. Indiana Univ. Math. J. 51 (2002), 1321–1338.CrossRefGoogle Scholar
Ioku, N.. The Cauchy problem for heat equations with exponential nonlinearity. J. Diff. Equ. 251 (2011), 1172–1194.CrossRefGoogle Scholar
Ioku, N., Ruf, B. and Terraneo, E.. Existence, non-existence, and uniqueness for a heat equation with exponential nonlinearity in $\mathbb {R}^{2}$. Math. Phys. Anal. Geom. 18 (2015), Art. 29, 19 pp.CrossRefGoogle Scholar
Kazdan, J. L. and Warner, F. W.. Curvature functions for compact 2-manifolds. Ann. Math. 99 (1974), 14–47.CrossRefGoogle Scholar
Kemppainen, J., Siljander, J., Vergara, V. and Zacher, R.. Decay estimates for time-fractional and other non-local in time subdiffusion equations in $\mathbb {R}^{d}$. Math. Ann. 366 (2016), 941–979.CrossRefGoogle Scholar
Kostianko, A. and Zelik, S.. Inertial manifolds for the 3D Cahn–Hilliard equations with periodic boundary conditions. Commun. Pure Appl. Anal. 14 (2015), 2069–2094.CrossRefGoogle Scholar
Liu, Liu S., Wang, F. and Zhao, H.. Global existence and asymptotics of solutions of the Cahn–Hilliard equation. J. Diff. Equ. 238 (2007), 426–469.CrossRefGoogle Scholar
Luca, L. D., Goldman, M. and Strani, M.. A gradient flow approach to relaxation rates for the multi-dimensional Cahn–Hilliard equation. Math. Ann. 374 (2019), 2041–2081.CrossRefGoogle Scholar
Mainardi, F.. Fractional calculus and waves in linear viscoelasticity: An introduction to mathematical models (London: World Scientific, 2010).CrossRefGoogle Scholar
Mainardi, F., Mura, A. and Pagnini, G.. The $M$-Wright function in time-fractional diffusion processes: a tutorial survey. Int. J. Diff. Equ. 2010 (2010), Art. ID 104505, 29 pp.Google Scholar
Nakamura, M. and Ozawa, T.. Nonlinear Schrödinger equations in the Sobolev space of critical order. J. Funct. Anal. 155 (1998), 364–380.CrossRefGoogle Scholar
Petropoulou, E. N.. On some difference equations with exponential nonlinearity. Discrete Contin. Dyn. Syst. Ser. B. 22 (2017), 2587–2594.Google Scholar
Robinson, J. C., Rodrigo, J. L. and Sadowski, W.. The three-dimensional Navier–Stokes equations. Cambridge Studies in Advanced Mathematics (Cambridge: Cambridge University Press, 2016).CrossRefGoogle Scholar
Temam, R.. Infinite dimensional dynamical systems in mechanics and physics. Applied Mathematical Sciences, vol. 68 (New York: Springer, 1988).CrossRefGoogle Scholar
Tuan, N. H., Nane, E., O'Regan, D. and Phuong, N. D.. Approximation of mild solutions of a semilinear fractional differential equation with random noise. Proc. Am. Math. Soc. 148 (2020), 3339–3357.CrossRefGoogle Scholar
Tuan, N. H., Ngoc, T. B., Zhou, Y. and O'Regan, D.. On existence and regularity of a terminal value problem for the time fractional diffusion equation. Inverse Problems 36 (2020), 055011, 41 pp.CrossRefGoogle Scholar
Tuan, N. H., Au, V. V. and Xu, R.. Semilinear Caputo time-fractional pseudo-parabolic equations. Commun. Pure Appl. Anal. 20 (2021), 583–621.CrossRefGoogle Scholar
Vergara, V. and Zacher, R.. Optimal decay estimates for time-fractional and other non-local subdiffusion equations via energy methods. SIAM J. Math. Anal. 47 (2015), 210–239.CrossRefGoogle Scholar
Wang, R. N., Chen, D. H and Xiao, T. J.. Abstract fractional Cauchy problems with almost sectorial operators. J. Diff. Equ. 252 (2012), 202–235.CrossRefGoogle Scholar
Xu, J., Zhang, Z. and Caraballo, T.. Mild solutions to time fractional stochastic 2D-Stokes equations with bounded and unbounded delay. J. Dyn. Diff. Equ. 19 (2019), 1–21.Google Scholar
Xu, J., Zhang, Z. and Caraballo, T.. Well-posedness and dynamics of impulsive fractional stochastic evolution equations with unbounded delay. Commun. Nonlinear Sci. Numer. Simul. 75 (2019), 121–139.CrossRefGoogle Scholar
Zacher, R.. Weak solutions of abstract evolutionary integro-differential equations in Hilbert spaces. Funkcialaj Ekvacioj 52 (2009), 1–18.CrossRefGoogle Scholar
Zacher, R., Time fractional diffusion equations: Solution concepts, regularity, and long-time behavior. In Handbook of fractional calculus with applications, vol. 2, pp. 159–179 (Berlin: De Gruyter, 2019).Google Scholar