Hostname: page-component-669899f699-qzcqf Total loading time: 0 Render date: 2025-04-30T03:56:55.307Z Has data issue: false hasContentIssue false
  • English
  • Français

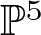On the Hilbert scheme of smooth curves of degree d = 15 in $\mathbb{P}^5$

Part of: Curves Cycles and subschemes

Published online by Cambridge University Press:  16 December 2024

Edoardo Ballico  and
Changho Keem
Edoardo Ballico
Affiliation:
Dipartimento di Matematica, Universita ‘degli Studi di Trento, Via Sommarive 14, 38123, Trento, Italy ([email protected])
Changho Keem*
Affiliation:
Department of Mathematics, Seoul National University, Seoul 151-742, South Korea ([email protected] and [email protected]) (corresponding author)
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

We denote by 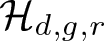$\mathcal{H}_{d,g,r}$ the Hilbert scheme of smooth curves, which is the union of components whose general point corresponds to a smooth, irreducible, and non-degenerate curve of degree d and genus g in 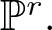$\mathbb{P}^r.$ In this article, we study 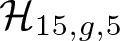$\mathcal{H}_{15,g,5}$ for every possible genus g and determine when it is irreducible. We also study the moduli map 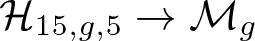$\mathcal{H}_{15,g,5}\rightarrow\mathcal{M}_g$ and several key properties such as gonality of a general element as well as characterizing smooth elements of each component.

Keywords

algebraic curvesarithmetically Cohen–MaaculayHilbert schemelinear seriesSeveri variety

MSC classification

Primary: 14C05: Parametrization (Chow and Hilbert schemes)
Secondary: 14H10: Families, moduli (algebraic)
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 38
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Accola, R.. Topics in the theory of Riemann surfaces, Lecture Notes in Mathematics 1595 (Springer, Heidelberg, 1991).Google Scholar
Arbarello, E. and Cornalba, M.. A few remarks about the variety of irreducible plane curves of given degree and genus. Ann. Sci. Éc. Norm. Supér. (4) 16(3) (1983), 467–483.CrossRefGoogle Scholar
Arbarello, E., Cornalba, M. and Griffiths, P.. Geometry of Algebraic Curves Vol. II (Springer, Heidelberg, 2011).CrossRefGoogle Scholar
Arbarello, E., Cornalba, M., Griffiths, P. and Harris, J.. Geometry of Algebraic Curves Vol. I (Springer-Verlag, Berlin/Heidelberg/New York/Tokyo, 1985).CrossRefGoogle Scholar
Ballico, E.. Interpolation of homogeneous polynomials over a finite field. Adv. Geom. 6 (2006), 215–224.CrossRefGoogle Scholar
Ballico, E., Fontanari, C. and Keem, C.. On the Hilbert scheme of linearly normal curves in $\mathbb{P}^r$ of relatively high degree. J. Pure Appl. Algebra 224 (2020), 1115–1123.CrossRefGoogle Scholar
Ballico, E. and Keem, C.. On the Hilbert scheme of smooth curves of degree 15 and genus 14 in ${\mathbb{P}}^5$. Bollettino UMI 17(3) (2024), CrossRefGoogle Scholar
Bernardi, A., Gimigliano, A. and Idà, M.. Computing symmetric rank for symmetric tensors. J. Symbolic. Comput. 46(1) (2011), 34–53.CrossRefGoogle Scholar
Brevik, J.. Curves on normal rational cubic surfaces. Pacific J. Math. 230(3) (2007), 73–105.CrossRefGoogle Scholar
Bruns, W. and Herzog, J.. Cohen-Macaulay Rings (Cambridge University Press, Cambridge, 1993).Google Scholar
Cho, K., Keem, C. and Park, S.. On the Hilbert scheme of trigonal curves and nearly extremal curves. Kyushu J. Math. 55(1) (2001), 1–12.CrossRefGoogle Scholar
Coppens, M.. The gonality of general smooth curves with a prescribed plane nodal model. Math. Ann. 289 (1991), 89–93.CrossRefGoogle Scholar
Coppens, M.. Embeddings of general blowing-ups at points. J. reine angew. Math. 469 (1995), 179–198.Google Scholar
Di Rocco, S.. k-very ample line bundles on Del-Pezzo surfaces. Math. Nachr. 179 (1996), 47–56.CrossRefGoogle Scholar
Dolgachev, I.. Classical Algebraic Geometry. A Modern View (Cambridge University Press, Cambridge, 2012), xii+639.CrossRefGoogle Scholar
Ein, L.. The irreducibility of the Hilbert scheme of complex space curves, Algebraic geometry, Bowdoin (Brunswick, Maine, 1985), Proc. Sympos. Pure Math., 46, 83–87 (Amer. Math. Soc., Providence, RI, 1985).CrossRefGoogle Scholar
Ein, L.. Hilbert scheme of smooth space curves. Ann. Scient. Ec. Norm. Sup. (4) 19(4) (1986), 469–478.CrossRefGoogle Scholar
Eisenbud, D.. Commutative Algebra with a View Toward Algebraic Geometry (Springer-Verlag, Berlin, 1995).Google Scholar
Harris, J.., Curves in projective space, 85 Séminaire de Mathématiques Supérieures (Montreal, Quebec: Presses de l’Université de Montréal, 1982). With the collaboration of D. Eisenbud.Google Scholar
Harris, J.. On the Severi problem. Invent. Math. 84(3) (1986), 445–461.CrossRefGoogle Scholar
Harris, J.. Brill-Noether theory. Geometry of Riemann surfaces and their moduli spaces, Surveys in Differential Geometry, XIV, 131–143 (Int. Press, Somerville, MA, 2009).Google Scholar
Hartshorne, R.. Algebraic Geometry (Springer-Verlag, Berlin/Heidelberg/New York, 1977).CrossRefGoogle Scholar
Hirschowitz, A.. La méthode d’Horace pour l’interpolation à plusieurs variables. Manuscripta Math. 50 (1985), 337–388.CrossRefGoogle Scholar
Kaplansky, I.. Commutative Rings (The University of Chicago Press, Chicago and London, 1974) rev. ed.Google Scholar
Keem, C.. Reducible Hilbert scheme of smooth curves with positive Brill-Noether number. Proc. A.M.S. 122(2) (1994), 349–354.CrossRefGoogle Scholar
Keem, C.. Existence and the reducibility of the Hilbert scheme of linearly normal curves in $\mathbb{P}^r$ of relatively high degrees. J. Pure Appl. Algebra 227 (2023), 1115–1123.CrossRefGoogle Scholar
Laface, A.. On linear systems of curves on rational scrolls. Geom. Dedicata 90 (2002), 127–144.CrossRefGoogle Scholar
Martens, G.. The gonality of curves on a Hirzebruch surface. Arch. Math. (Basel) 67 (1996), 349–352.CrossRefGoogle Scholar
Martens, G. and Schreyer, F.-O.. Line bundles and syzygies of trigonal curves. Abh. Math. Sem. Univ. Hamburg 56 (1985), 169–189.CrossRefGoogle Scholar
Matsumura, H.. Commutative Ring Theory (Cambridge University Press, Cambridge, 1989).Google Scholar
Migliore, J.. Introduction to liaison theory and deficiency modules, Progress in Mathematics, 165 (Berlin: Springer Science, 1998).Google Scholar
Paxia, G., Raciti, G. and Ragusa, A.. On the Lüroth semigroup of curves lying on a smooth quadric. Manuscripta Math. 75(1) (1992), 225–246.CrossRefGoogle Scholar
Severi, F.. Vorlesungen über Algebraische Geometrie (Teubner, Leipzig, 1921).CrossRefGoogle Scholar
Tyomkin, I.. (2007) On Severi varieties on Hirzebruch surfaces. Int. Math. Res. Not. 23(9), .Google Scholar