Hostname: page-component-669899f699-tzmfd Total loading time: 0 Render date: 2025-04-25T17:37:15.840Z Has data issue: false hasContentIssue false
  • English
  • Français

On the continuity of the polyconvex, quasiconvex and rank-oneconvex envelopes with respect to growth condition

Published online by Cambridge University Press:  14 November 2011

Wilfrid Gangbo
Wilfrid Gangbo
Affiliation:
Ecole Polytechnique Federate de Lausanne, 1015 Lausanne, Switzerland
Get access Rights & Permissions [Opens in a new window]

Synopsis

Let Cf, Pf, Qf and Rf be respectively the convex, polyconvex, quasi-convex and rank-one-convex envelopes of a given function f. If fp: RNxM→R and fq(ξ) behaves as |ξ|q at infinity q ∈ (1, ∞), we show that 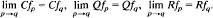. This is the case for (Pfp)p provided that q ≠1,…, min (N, M), otherwise 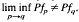. In the last part of this work, we show that f(ξ) = g(|ξ|) does not imply in general Pf = Qf.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 123 , Issue 4 , 1993 , pp. 707 - 729
Copyright
Copyright © Royal Society of Edinburgh 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

1Alibert, J. J. and Dacorogna, B.. An example of a quasiconvex function that is not polyconvex in two dimension. Arch. Rational Mech. Anal. 117 (1992) 155–166.Google Scholar
2Ball, J. M.. Convexity conditions and existence theorems in nonlinear elasticity. Arch. Rational Mech. Anal. 64 (1977), 337–403.Google Scholar
3Brezis, H.. Analyse Fonctionnelle (Paris: Masson, 1983).Google Scholar
4Dacorogna, B.. Direct Methods in the Calculus of Variations (Berlin: 1989).Google Scholar
5Ekeland, I.. Non convex minimization problem. Bull. Amer. Math. Soc. 1 (3) (1979) 443–474.CrossRefGoogle Scholar
6Gehring, F.. The Lp integrability of the partial derivatives of quasiconformal mapping. Ada Math. 130 (1973), 265–277.Google Scholar
7Giaquinta, M. and Modica, G.. Regularity results for some classes of higher order non linear elliptic systems. J. Reine Angew. Math. 311/312 (1979), 145–169.Google Scholar
8Kohn, R. V.. The relaxation of a double-well energy (to appear).Google Scholar
9Kohn, R. V. and Strang, G.. Optimal design and relaxation of variational problems I, II and III. Comm. Pure Appl. Math. 39 (1986), 113–137; 139–182; 353–377.CrossRefGoogle Scholar
10Marcellini, P. and Sbordone, C.. On the existence of minima of multiple integrals. J. Math. Pures Appl. 62 (1983), 1–9.Google Scholar
11Morrey, C. B.. Quasiconvexity and semicontinuity of multiple integrales. Pacific J. Math. 2 (1952), 25–53.Google Scholar
12Morrey, C. B.. Multiple Integrals in the Calculus of Variations (Berlin: Springer, 1966).Google Scholar
13Simader, C. G.. On Dirichlet's Boundary Value Problem, Lecture Notes in Math. 268 (Berlin: Springer, 1972).Google Scholar
14Sverak, V.. Quasiconvex functions with subquadratic growth (to appear).Google Scholar