Hostname: page-component-669899f699-ggqkh Total loading time: 0 Render date: 2025-04-25T17:45:29.565Z Has data issue: false hasContentIssue false
  • English
  • Français

On Lebesgue points of entropy solutions to the eikonal equation

Part of: General first-order equations and systems Partial differential equations

Published online by Cambridge University Press:  23 May 2023

Xavier Lamy Open the ORCID record for Xavier Lamy [Opens in a new window]  and
Elio Marconi Open the ORCID record for Elio Marconi [Opens in a new window]
Xavier Lamy
Affiliation:
Institut de Mathématiques de Toulouse, UMR 5219, Université de Toulouse, CNRS, UPS IMT, F-31062 Toulouse Cedex 9, France ([email protected])
Elio Marconi
Affiliation:
Dipartimento di Matematica ‘Tullio Levi Civita’, Università di Padova, via Trieste 63, 35121 Padova, PD, Italy ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider entropy solutions to the eikonal equation $|\nabla u|=1$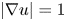 in two-space dimensions. These solutions are motivated by a class of variational problems and fail in general to have bounded variation. Nevertheless, they share several of their fine properties with BV functions: we show in particular that the set of non-Lebesgue points has at least one co-dimension.

Keywords

Aviles–Gigaeikonal equationLagrangian representation

MSC classification

Primary: 35F20: Nonlinear first-order equations
Secondary: 35B65: Smoothness and regularity of solutions
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 154 , Issue 4 , August 2024 , pp. 1047 - 1059
Check for updates
Copyright
Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adams, D. R. and Hedberg, L. I.. Function spaces and potential theory. Grundlehren Math. Wiss., vol. 314 (Berlin: Springer-Verlag, 1995).10.1007/978-3-662-03282-4CrossRefGoogle Scholar
Alouges, F., Rivière, T. and Serfaty, S.. Néel and cross-tie wall energies for planar micromagnetic configurations. ESAIM Control Optim. Calc. Var. 8 (2002), 31–68. A tribute to J. L. Lions.10.1051/cocv:2002017CrossRefGoogle Scholar
Ambrosio, L., De Lellis, C. and Mantegazza, C.. Line energies for gradient vector fields in the plane. Calc. Var. Partial Differ. Equ. 9 (1999), 327–255.10.1007/s005260050144CrossRefGoogle Scholar
Ambrosio, L., Fusco, N. and Pallara, D.. Functions of bounded variation and free discontinuity problems. Oxford Mathematical Monographs (New York: The Clarendon Press, Oxford University Press, 2000).10.1093/oso/9780198502456.001.0001CrossRefGoogle Scholar
Aviles, P. and Giga, Y.. A mathematical problem related to the physical theory of liquid crystal configurations. In Miniconference on Geometry and Partial Differential Equations, 2 (Canberra, 1986), Proc. Centre Math. Anal. Austral. Nat. Univ., vol. 12, pp. 1–16 (Canberra: Austral. Nat. Univ., 1987).Google Scholar
Contreras Hip, A. A., Lamy, X. and Marconi, E.. Generalized characteristics for finite entropy solutions of Burgers’ equation. Nonlinear Anal. 219 (2022), 112804.10.1016/j.na.2022.112804CrossRefGoogle Scholar
De Lellis, C. and Otto, F.. Structure of entropy solutions to the eikonal equation. J. Eur. Math. Soc. 5 (2003), 107–145.10.1007/s10097-002-0048-7CrossRefGoogle Scholar
DeSimone, A., Müller, S., Kohn, R. V. and Otto, F.. A compactness result in the gradient theory of phase transitions. Proc. R. Soc. Edinburgh Sect. A 131 (2001), 833–844.10.1017/S030821050000113XCrossRefGoogle Scholar
Ghiraldin, F. and Lamy, X.. Optimal Besov differentiability for entropy solutions of the eikonal equation. Commun. Pure Appl. Math. 73 (2020), 317–349.10.1002/cpa.21868CrossRefGoogle Scholar
Jabin, P.-E. and Perthame, B.. Compactness in Ginzburg–Landau energy by kinetic averaging. Commun. Pure Appl. Math. 54 (2001), 1096–1109.10.1002/cpa.3005CrossRefGoogle Scholar
Jin, W. and Kohn, R. V.. Singular perturbation and the energy of folds. J. Nonlinear Sci. 10 (2000), 355–390.10.1007/s003329910014CrossRefGoogle Scholar
Lamy, X. and Marconi, E.. Stability of the vortex in micromagnetics and related models. 2022, arXiv:2209.09662.10.2422/2036-2145.202209_012CrossRefGoogle Scholar
Lamy, X. and Otto, F.. On the regularity of weak solutions to Burgers’ equation with finite entropy production. Calc. Var. Partial Differ. Equ. 57 (2018), 4.10.1007/s00526-018-1380-4CrossRefGoogle Scholar
Marconi, E.. Characterization of minimizers of Aviles–Giga functionals in special domains. Arch. Ration. Mech. Anal. 242 (2021), 1289–1316.10.1007/s00205-021-01704-wCrossRefGoogle ScholarPubMed
Marconi, E.. Rectifiability of entropy defect measures in a micromagnetics model. Adv. Calc. Var. 16 (2021), 233–257.10.1515/acv-2021-0012CrossRefGoogle Scholar
Marconi, E.. On the structure of weak solutions to scalar conservation laws with finite entropy production. Calc. Var. Partial Differ. Equ. 61 (2022), 30. Id/No 32.10.1007/s00526-021-02137-9CrossRefGoogle Scholar
Rivière, T. and Serfaty, S.. Limiting domain wall energy for a problem related to micromagnetics. Commun. Pure Appl. Math. 54 (2001), 294–338.10.1002/1097-0312(200103)54:3<294::AID-CPA2>3.0.CO;2-S3.0.CO;2-S>CrossRefGoogle Scholar