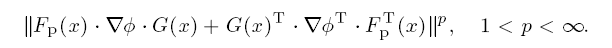Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Neff, Patrizio
2003.
Deformation and Failure in Metallic Materials.
Vol. 10,
Issue. ,
p.
251.
Neff, Patrizio
2004.
Existence of minimizers for a geometrically exact Cosserat solid.
PAMM,
Vol. 4,
Issue. 1,
p.
548.
Neff, P.
2004.
A geometrically exact Cosserat shell-model including size effects, avoiding degeneracy in the thin shell limit. Part I: Formal dimensional reduction for elastic plates and existence of minimizers for positive Cosserat couple modulus.
Continuum Mechanics and Thermodynamics,
Vol. 16,
Issue. 6,
p.
577.
Neff, Patrizio
2005.
Local existence and uniqueness for a geometrically exact membrane-plate with viscoelastic transverse shear resistance.
Mathematical Methods in the Applied Sciences,
Vol. 28,
Issue. 9,
p.
1031.
Neff, P.
2006.
The Cosserat couple modulus for continuous solids is zero viz the linearized Cauchy-stress tensor is symmetric.
ZAMM,
Vol. 86,
Issue. 11,
p.
892.
Ten Eyck, A.
and
Lew, A.
2006.
Discontinuous Galerkin methods for non-linear elasticity.
International Journal for Numerical Methods in Engineering,
Vol. 67,
Issue. 9,
p.
1204.
NEFF, PATRIZIO
2007.
A GEOMETRICALLY EXACT PLANAR COSSERAT SHELL-MODEL WITH MICROSTRUCTURE: EXISTENCE OF MINIMIZERS FOR ZERO COSSERAT COUPLE MODULUS.
Mathematical Models and Methods in Applied Sciences,
Vol. 17,
Issue. 03,
p.
363.
Neff, Patrizio
and
Münch, Ingo
2008.
Curl bounds Grad on SO(3).
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 14,
Issue. 1,
p.
148.
Neff, Patrizio
2010.
Poly-, Quasi- and Rank-One Convexity in Applied Mechanics.
Vol. 516,
Issue. ,
p.
301.
Tambača, Josip
and
Velčić, Igor
2010.
Semicontinuity theorem in the micropolar elasticity.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 16,
Issue. 2,
p.
337.
Tambača, Josip
and
Velčić, Igor
2010.
Existence theorem for nonlinear micropolar elasticity.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 16,
Issue. 1,
p.
92.
Neff, Patrizio
Pauly, Dirk
and
Witsch, Karl-Josef
2011.
A canonical extension of Kornʼs first inequality to H(Curl) motivated by gradient plasticity with plastic spin.
Comptes Rendus. Mathématique,
Vol. 349,
Issue. 23-24,
p.
1251.
Pompe, Waldemar
2011.
Counterexamples to Korn’s inequality with non-constant rotation coefficients.
Mathematics and Mechanics of Solids,
Vol. 16,
Issue. 2,
p.
172.
Klawonn, Axel
Neff, Patrizio
Rheinbach, Oliver
and
Vanis, Stefanie
2011.
FETI-DP domain decomposition methods for elasticity with structural changes:P-elasticity.
ESAIM: Mathematical Modelling and Numerical Analysis,
Vol. 45,
Issue. 3,
p.
563.
Neff, P.
Pauly, D.
and
Witsch, K.-J.
2012.
On a canonical extension of Korn’s first and Poincaré’s inequalities to H(CURL).
Journal of Mathematical Sciences,
Vol. 185,
Issue. 5,
p.
721.
Dias, Gilberlandio J.
and
Santos, Marcelo M.
2012.
Steady flow for shear thickening fluids with arbitrary fluxes.
Journal of Differential Equations,
Vol. 252,
Issue. 6,
p.
3873.
Lankeit, Johannes
Neff, Patrizio
and
Pauly, Dirk
2013.
Uniqueness of Integrable Solutions ∇ζ = Gζ, ζ∣Γ = 0 for Integrable Tensor‐Coefficients G and Applications to Elasticity.
PAMM,
Vol. 13,
Issue. 1,
p.
361.
Lankeit, Johannes
Neff, Patrizio
and
Pauly, Dirk
2013.
Unique continuation for first-order systems with integrable coefficients and applications to elasticity and plasticity.
Comptes Rendus. Mathématique,
Vol. 351,
Issue. 5-6,
p.
247.
Lankeit, Johannes
Neff, Patrizio
and
Pauly, Dirk
2013.
Uniqueness of integrable solutions to $${\nabla \zeta=G \zeta, \zeta|_\Gamma = 0}$$ for integrable tensor coefficients G and applications to elasticity.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 64,
Issue. 6,
p.
1679.
Bîrsan, Mircea
and
Altenbach, Holm
2013.
On the Cosserat model for thin rods made of thermoelastic materials with voids.
Discrete and Continuous Dynamical Systems - Series S,
Vol. 6,
Issue. 6,
p.
1473.




 which is just our result with Fp = 11. With slight modifications, we are also able to treat forms of the type
which is just our result with Fp = 11. With slight modifications, we are also able to treat forms of the type