Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-22T12:31:05.496Z Has data issue: false hasContentIssue false
  • English
  • Français

On inhomogeneous biharmonic equations involving critical exponents

Published online by Cambridge University Press:  14 November 2011

Yinbin Deng  and
Gengsheng Wang
Yinbin Deng
Affiliation:
Department of Mathematics Huazhong Normal University Wuhan 430079 People'sRepublic of China ([email protected])
Gengsheng Wang
Affiliation:
Department of Mathematics Huazhong Normal University Wuhan 430079 People'sRepublic of China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we consider the existence of multiple solutions of biharmonic equations boundary value problem

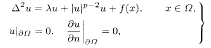
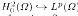where Ω is a bounded smooth domain in ℝN, N ≥ 5; λ ∈ ℝ1 is a given constant; p = 2N/(N − 4) is the critical Sobolev exponent for the embedding ; Δ2 = ΔΔ denotes iterated N-dimensional Laplacian; f(x) is a given function. Some results on the existence and non-existence of multiple solutions for the above problem have been obtained by Ekeland's variational principle and the mountain-pass lemma under some assumptions on f(x) and N.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 129 , Issue 5 , 1999 , pp. 925 - 946
Copyright
Copyright © Royal Society of Edinburgh 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Aubin, J. P. and Ekeland, I.. Applied nonlinear analysis. Pure and Applied Mathematics (Wiley, 1984).Google Scholar
2Berni, F., Garcia-Azorero, s. J. and Peral, I.. Existence and multiplicity of nontrival solutions in semilinear critical problems of fourth order. Adv. Diff. Eqns 1 (1996). 219–240.Google Scholar
3Bernis, F. and Grunau, H. C.. Critical exponents and multiple critical dimensions for polyharmonic operators. J. Diff. Eqns 117 (1995), 469–486.CrossRefGoogle Scholar
4Brezis, H. find Lieb, E. H.. A relation between pointwise convergence of functions and convergence of functional. Proc. Am. Math. Soc. 88 (1983), 486–490.CrossRefGoogle Scholar
5Brezis, H. and Nirenberg, L.. A minimization problem with critical exponent and non zero data. In Symmetry in nature (Pisa: Scuola Norm. Sup., 1989).Google Scholar
6Brezis, H. and Nirenberg, L.. Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents. Commun. Pure. Appl. Math. 36 (1983), 437–477.CrossRefGoogle Scholar
7Cao, D. M.. Li, G. B. and Zhou, H. S.. Multiple solutions for nonhomogeneous elliptic equations involving critical sobolev exponent. Proc. R. Soc. Edinb. A 124 (1994), 1177–1191.CrossRefGoogle Scholar
8Cerami, G.. Solimini, S. and Struwe, M.. Some existence results for superlinear elliptic boundary value problem involving Sobolev exponents. J. Funct. Analysis 69 (1986), 389.CrossRefGoogle Scholar
9Deng, Y. B.. Existence of multiple positive solutions for −Δu = λu + u (N + 2)/(N − 2) + μf(x). Acta Math. Sinica 9(3) (1993), 311–320.Google Scholar
10Deng, Y. B.. Existence of multiple positive solutions of inhomogeneous semilinear elliptic problem involving critical exponents. Commun. PDE 17(1–2) (1992). 33–53.CrossRefGoogle Scholar
11Deng, Y. B. and Li, Y.. Existence and bifurcation of the positive solutions for a semilinear elliptic equation with critical exponent. J. Diff. Eqns 130 (1996), 179–200.CrossRefGoogle Scholar
12Deng, Y. B. and Yang, J. F.. Existence of multiple solutions and bifurcation for critical semilinear biharmonic equation. Syst. Sci. Math. Sci. 8 (1995). 319–326.Google Scholar
13Edmunds, D. E.. Fortunato, D. and Jannelli, E.. Critical dimensions and the biharmonic operator. Arch. Ration. Mech. Analysis 112 (1990), 269–289.CrossRefGoogle Scholar
14Grunau, H. C.. Positive solutions to semilinear polyharnionic Dirichlet problems involving critical Sobolev exponents. Calc. Var. PDE 3 (1995), 234–252.CrossRefGoogle Scholar
15Grunau, H. C.. Critical exponents and multiple critical dimensions for polyharmonic operators. Boll. Un. Mat. Ital. B 9 (1995), 815–847.Google Scholar
16Grunau, H. C.. On the conjecture of P. Pucci and J. Serriri. Analysis 16 (1996), 399–403.CrossRefGoogle Scholar
17Gu, Y. G., Deng, Y. B. and Wang, X. J.. Existence of nontrivial solutions for critical semilinear biharmonk equations. Syst. Sci. Math. Sci. 72 (1994). 140–152.Google Scholar
18Noussair, E. S., Swanson, C. A. and Yang, J. F.. Critical semilinear biharmonic equations in ℝN. Proc. R. Soc. Edinb. A 121 (1992). 139–148.CrossRefGoogle Scholar
19Pucci, P. and Serrin, J.. A general variational identity. Indiana Univ. Math. J. 35 (1986). 681–703.CrossRefGoogle Scholar
20Pucci, P. and Serrin, J.. Critical exponents and critical dimensions for polyharmonic operators. J. Math. Pures Appl. 69 (1990), 55–83.Google Scholar
21Tarantello, G.. On nonhomogeneous elliptic equations involving critical Sobolev's exponent. Ann. Inst. Henri Poincaré 9(3) (1992). 281–304.CrossRefGoogle Scholar
22Yang, J. F.. Positive solutions of semilinear elliptic problems in exterior domains. J. Diff. Eqns 106 (1993). 49–69.CrossRefGoogle Scholar