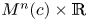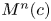Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Albujer, Alma L.
da Silva, Sylvia F.
and
dos Santos, Fábio R.
2023.
Total mean curvature surfaces in the product space and applications.
Proceedings of the Edinburgh Mathematical Society,
Vol. 66,
Issue. 2,
p.
346.
SANTOS, FÁBIO R. DOS
SILVA, SYLVIA F. DA
and
SOUSA, ANTONIO F. DE
2023.
Integral inequalities for closed linear Weingarten submanifolds in the product spaces.
Anais da Academia Brasileira de Ciências,
Vol. 95,
Issue. 3,
Qiu, Wang-Hua
and
Zhan, Xin
2023.
Curvature Pinching Problems for Compact Pseudo-Umbilical PMC Submanifolds in Sm(c)×R.
Mathematics,
Vol. 12,
Issue. 1,
p.
68.
dos Santos, Fábio R.
and
Cruz, Joicy P.
2025.
On the stochastically complete hypersurfaces in the product spaces Mn(κ)×R.
Journal of Mathematical Analysis and Applications,
Vol. 546,
Issue. 2,
p.
129292.