Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lupulescu, Afina
Glicksman, Martin
and
Koss, Matthew
2004.
Mushy Zones Evolution Under Microgravity Conditions.
Lupulescu, A.
Glicksman, M.E.
and
Koss, M.B.
2005.
Conduction-limited crystallite melting.
Journal of Crystal Growth,
Vol. 276,
Issue. 3-4,
p.
549.
Mccue, Scott W.
King, John R.
and
Riley, David S.
2005.
The Extinction Problem for Three-dimensional Inward Solidification.
Journal of Engineering Mathematics,
Vol. 52,
Issue. 4,
p.
389.
Lupulescu, Afina
Glicksman, Martin
and
Koss, Matthew
2005.
Capillarity Effects In Mushy Zones Under Microgravity Conditions.
Glicksman, M. E.
Lupulescu, A.
and
Koss, M. B.
2006.
Free Boundary Problems.
Vol. 154,
Issue. ,
p.
219.
Glicksman, Martin
Lupulescu, Afina
Salon, S.
Kwon, O.
and
Koss, Matthew
2006.
Late-Stage Capillarity Effects During Crystallite Melting in Microgravity.
Wu, Bisheng
McCue, Scott W.
Tillman, Pei
and
Hill, James M.
2009.
Single phase limit for melting nanoparticles.
Applied Mathematical Modelling,
Vol. 33,
Issue. 5,
p.
2349.
Back, Julian M.
McCue, Scott W.
and
Moroney, Timothy J.
2014.
Including nonequilibrium interface kinetics in a continuum model for melting nanoscaled particles.
Scientific Reports,
Vol. 4,
Issue. 1,
Back, Julian M.
McCue, Scott W.
Hsieh, Mike H.-N.
and
Moroney, Timothy J.
2014.
The effect of surface tension and kinetic undercooling on a radially-symmetric melting problem.
Applied Mathematics and Computation,
Vol. 229,
Issue. ,
p.
41.
Myers, T.G.
and
Font, F.
2015.
On the one-phase reduction of the Stefan problem with a variable phase change temperature.
International Communications in Heat and Mass Transfer,
Vol. 61,
Issue. ,
p.
37.
Shkolnikov, Mykhaylo
Mete Soner, H.
and
Tissot-Daguette, Valentin
2024.
Deep level-set method for Stefan problems.
Journal of Computational Physics,
Vol. 503,
Issue. ,
p.
112828.
Zhang, Chencheng
2025.
On melting for the 3D radial Stefan problem.
Calculus of Variations and Partial Differential Equations,
Vol. 64,
Issue. 3,
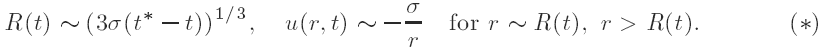 Here, R(t) denotes the radius of the crystal, σ is a surface tension parameter and u(r, t) represents the field temperature. An important point to be noticed is that (*) exhibits no dependence on the space dimension N, in sharp contrast with results known for the case σ = 0.
Here, R(t) denotes the radius of the crystal, σ is a surface tension parameter and u(r, t) represents the field temperature. An important point to be noticed is that (*) exhibits no dependence on the space dimension N, in sharp contrast with results known for the case σ = 0.