Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Neamaty, A.
and
Haghaieghy, S.
2009.
On the asymptotic of an eigenvalue problem with 2n interior singularities.
Proceedings - Mathematical Sciences,
Vol. 119,
Issue. 5,
p.
619.
Hormozi, Mahdi
2012.
A note on a paper of Harris concerning the asymptotic approximation to the eigenvalues of -y'' + qy = λy, with boundary conditions of general form.
Boundary Value Problems,
Vol. 2012,
Issue. 1,


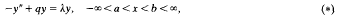
 . We extend Atkinson's results to cover more singular
. We extend Atkinson's results to cover more singular