Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-19T11:22:06.723Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-trivial solutions of elliptic equations at resonance

Published online by Cambridge University Press:  14 November 2011

Klaus Thews
Klaus Thews
Affiliation:
Mathematisches Seminar der Christian-Albrechts-Universität Kiel, Olshausenstr. 40–60, D-2300 Kiel, B.R.D.
Get access Rights & Permissions [Opens in a new window]

Synopsis

In this paper we show that Dirichlet problems at resonance, being of the type −Δu(x) = λku(x) + g(u(x)), x є G, u(x) = 0 for x є ∂G, g(−u) = −g(u), admit multiple non-trivial solutions provided the non-linearity interacts in some sense with the spectrum of −Δ. In contrast to other work on this subject we deal with the case that g(u) is very small for large arguments, for instance g(u) = 0 for |u| large. 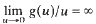On the other hand if and g satisfies a certain concavity condition at 0 the existence of infinitely many solutions is shown independent of the asymptotic behaviour of g.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 85 , Issue 1-2 , 1980 , pp. 119 - 129
Copyright
Copyright © Royal Society of Edinburgh 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Ahmad, S., Lazer, A. C. and Paul, J. L.. Elementary critical point theory and perturbations of elliptic boundary value problems at resonance. Indiana Univ. Math. J. 25 (1976), 933–944.CrossRefGoogle Scholar
2Ambrosetti, A.. Esistenza di infinite soluzioni per problemi non lineari in assenza di parametro. Afri Accod. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Natur. 52 (1972), 660–667.Google Scholar
3Ambrosetti, A. and Mancini, G.. Theorems of existence and multiplicity for nonlinear elliptic problems with noninvertible linear part. Ann. Scuola Norm. Sup. Pisa 5 (1978), 15–28.Google Scholar
4.Ambrosetti, A. and Rabinowitz, P. H.. Dual variational methods in critical point theory and application. J. Functional Analysis 14 (1973), 349–381.CrossRefGoogle Scholar
5Clark, D. C.. A variant of the Lusternik-Schnirelman theory. Indiana Univ. Math. J. 22 (1972), 65–74.CrossRefGoogle Scholar
6Hempel, J.. Superlinear variational boundary value problems and nonuniqueness. (Thesis, Univ. of New England, Australia, 1970).Google Scholar
7Mizohata, S.. The theory of partial differential equations (Cambridge Univ. Press, 1973).Google Scholar
8Rabinowitz, P. H.. Some minimax theorems and applications to nonlinear partial differential equations. In Nonlinear analysis. A collection of papers in honor of Rothe, Erich H., ed. Cesari, L., Kannán, R., Weinberger, H. F. (New York/San Francisco/London: Academic Press, 1978).Google Scholar
9Reeken, M.. Stability of critical points under small perturbations I. Manuscripta Math. 7 (1972), 387–411.CrossRefGoogle Scholar
10Thews, K.. Multiple solutions for elliptic boundary value problems with odd nonlinearities. Math. Z. 163 (1978), 163–175.CrossRefGoogle Scholar
11Thews, K.. A reduction method for some nonlinear Dirichlet problems. J. Nonlinear Analysis, to appear.Google Scholar