Published online by Cambridge University Press: 26 January 2019
We prove that the fractional Yamabe equation 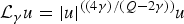 ${\rm {\cal L}}_\gamma u = \vert u \vert ^{((4\gamma )/(Q-2\gamma ))}u$ on the Heisenberg group ℍn has [n + 1/2] sequences of nodal (sign-changing) weak solutions whose elements have mutually different nodal properties, where
${\rm {\cal L}}_\gamma u = \vert u \vert ^{((4\gamma )/(Q-2\gamma ))}u$ on the Heisenberg group ℍn has [n + 1/2] sequences of nodal (sign-changing) weak solutions whose elements have mutually different nodal properties, where 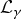 ${\rm {\cal L}}_\gamma $ denotes the CR fractional sub-Laplacian operator on ℍn, Q = 2n + 2 is the homogeneous dimension of ℍn, and
${\rm {\cal L}}_\gamma $ denotes the CR fractional sub-Laplacian operator on ℍn, Q = 2n + 2 is the homogeneous dimension of ℍn, and 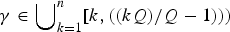 $\gamma \in \bigcup\nolimits_{k = 1}^n [k,((kQ)/Q-1)))$. Our argument is variational, based on a Ding-type conformal pulling-back transformation of the original problem into a problem on the CR sphere S2n + 1 combined with a suitable Hebey-Vaugon-type compactness result and group-theoretical constructions for special subgroups of the unitary group U(n + 1).
$\gamma \in \bigcup\nolimits_{k = 1}^n [k,((kQ)/Q-1)))$. Our argument is variational, based on a Ding-type conformal pulling-back transformation of the original problem into a problem on the CR sphere S2n + 1 combined with a suitable Hebey-Vaugon-type compactness result and group-theoretical constructions for special subgroups of the unitary group U(n + 1).
Dedicated to Professor Patrizia Pucci on the occasion of her 65th birthday.