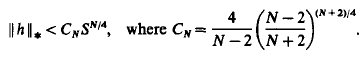Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Deng, Yinbin
and
Wang, Gengsheng
1999.
On inhomogeneous biharmonic equations involving critical exponents.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 129,
Issue. 5,
p.
925.
Alves, C.O.
Marcos do Ó, João
and
Miyagaki, O.H.
2001.
Nontrivial solutions for a class of semilinear biharmonic problems involving critical exponents.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 46,
Issue. 1,
p.
121.
Alves, Claudianor Oliveira
Carrião, Paulo Cesar
and
Miyagaki, Olimpio Hiroshi
2001.
Nonlinear Perturbations of a Periodic Elliptic Problem with Critical Growth.
Journal of Mathematical Analysis and Applications,
Vol. 260,
Issue. 1,
p.
133.
Pei-hao, Zhao
Cheng-kui, Zhong
and
Jiang, Zhu
2001.
Positive Solutions for a Nonhomogeneous Semilinear Elliptic Problem with Supercritical Exponent.
Journal of Mathematical Analysis and Applications,
Vol. 254,
Issue. 2,
p.
335.
Tan, Zhong
and
Yao, Zhengan
2001.
The existence of multiple solutions of p -laplacian elliptic equation.
Acta Mathematica Scientia,
Vol. 21,
Issue. 2,
p.
203.
Huang, Yi Sheng
2001.
Multiple positive solutions of nonhomogeneous equations involving the p-Laplacian.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 43,
Issue. 7,
p.
905.
Wang, Zhengping
and
Zhou, Huansong
2006.
SOLUTIONS FOR A NONHOMOGENEOUS ELLIPTIC PROBLEM INVOLVING CRITICAL SOBOLEV-HARDY EXPONENT IN RN.
Acta Mathematica Scientia,
Vol. 26,
Issue. 3,
p.
525.
Dai, Qiuyi
and
Peng, Lihui
2007.
Necessary and sufficient conditions for the existence of nonnegative solutions of inhomogeneous p-Laplace equation.
Acta Mathematica Scientia,
Vol. 27,
Issue. 1,
p.
34.
Assunção, Ronaldo B.
Carrião, Paulo Cesar
and
Miyagaki, Olimpio Hiroshi
2007.
Critical singular problems via concentration-compactness lemma.
Journal of Mathematical Analysis and Applications,
Vol. 326,
Issue. 1,
p.
137.
Liu, Haidong
2009.
Multiple positive solutions for a semilinear elliptic equation with critical Sobolev exponent.
Journal of Mathematical Analysis and Applications,
Vol. 354,
Issue. 2,
p.
451.
de Freitas, Luciana R.
2014.
Multiplicity of solutions for a class of quasilinear equations with exponential critical growth.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 95,
Issue. ,
p.
607.
Ba, Na
Wang, Yan-yan
and
Zheng, Lie
2016.
Multiplicity and uniqueness of positive solutions for nonhomogeneous semilinear elliptic equation with critical exponent.
Acta Mathematicae Applicatae Sinica, English Series,
Vol. 32,
Issue. 1,
p.
81.
Liao, Jia-feng
Liu, Jiu
Zhang, Peng
and
Tang, Chun-Lei
2016.
Existence and multiplicity of positive solutions for a class of elliptic equations involving critical Sobolev exponents.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 110,
Issue. 2,
p.
483.
Xiang, Mingqi
Zhang, Binlin
and
Zhang, Xia
2017.
A Nonhomogeneous Fractional p-Kirchhoff Type Problem Involving Critical Exponent in ℝ
N
.
Advanced Nonlinear Studies,
Vol. 17,
Issue. 3,
p.
611.
Zhang, Jing
and
Ma, Shiwang
2017.
On nonhomogeneous elliptic problems involving the Hardy potential and critical Sobolev exponent.
Rocky Mountain Journal of Mathematics,
Vol. 47,
Issue. 2,
Xiang, MingQi
Zhang, BinLin
and
Qiu, Hong
2017.
Existence of solutions for a critical fractional Kirchhoff type problem in ℝ N.
Science China Mathematics,
Vol. 60,
Issue. 9,
p.
1647.
LIAO, Jiafeng
PU, Yang
and
TANG, Chunlei
2018.
Multiplicity of positive solutions for a class of concave-convex elliptic equations with critical growth.
Acta Mathematica Scientia,
Vol. 38,
Issue. 2,
p.
497.
Lin, Xiaolu
and
Zheng, Shenzhou
2021.
Multiplicity and asymptotic behavior of solutions to fractional (p,q)-Kirchhoff type problems with critical Sobolev-Hardy exponent.
Electronic Journal of Differential Equations,
Vol. 2021,
Issue. 01-104,
p.
66.
Boukarabila, Youssouf Oussama
Nasri, Yasmina
and
Senhadji, Asma
2022.
Critical problem for the fractional Laplacian operator with sign changing data.
Complex Variables and Elliptic Equations,
Vol. 67,
Issue. 9,
p.
2181.
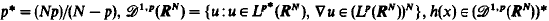 is continuous on RN and h(x)≢0. By using Ekeland's variational principle and the Mountain Pass Theorem without (PS) conditions, through a careful inspection of the energy balance for the approximated solutions, we show that the probelm (*) has at least two solutions for some λ* > 0 and λ ∈ (0, λ*). In particular, if p = 2, in a different way we prove that problem (*) with λ ≡ 1 and h(x) ≧ 0 has at least two positive solutions as
is continuous on RN and h(x)≢0. By using Ekeland's variational principle and the Mountain Pass Theorem without (PS) conditions, through a careful inspection of the energy balance for the approximated solutions, we show that the probelm (*) has at least two solutions for some λ* > 0 and λ ∈ (0, λ*). In particular, if p = 2, in a different way we prove that problem (*) with λ ≡ 1 and h(x) ≧ 0 has at least two positive solutions as