Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-17T18:19:44.082Z Has data issue: false hasContentIssue false
  • English
  • Français

Multi-peak positive solutions to a class of Kirchhoff equations

Part of: Partial differential equations Elliptic equations and systems

Published online by Cambridge University Press:  27 December 2018

Peng Luo ,
Shuangjie Peng ,
Chunhua Wang  and
Chang-Lin Xiang
Peng Luo
Affiliation:
School of Mathematics and Statistics and Hubei Key Laboratory of Mathematical Sciences, Central China Normal University, Wuhan, 430079, P.R. China ([email protected]; [email protected]; [email protected])
Shuangjie Peng
Affiliation:
School of Mathematics and Statistics and Hubei Key Laboratory of Mathematical Sciences, Central China Normal University, Wuhan, 430079, P.R. China ([email protected]; [email protected]; [email protected])
Chunhua Wang
Affiliation:
School of Mathematics and Statistics and Hubei Key Laboratory of Mathematical Sciences, Central China Normal University, Wuhan, 430079, P.R. China ([email protected]; [email protected]; [email protected])
Chang-Lin Xiang
Affiliation:
School of Information and Mathematics, Yangtze University, Jingzhou, 434023, P.R. China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In the present paper, we consider the nonlocal Kirchhoff problem

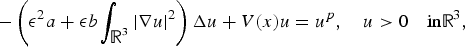$$-\left(\epsilon^2a+\epsilon b\int_{{\open R}^{3}}\vert \nabla u \vert^{2}\right)\Delta u+V(x)u=u^{p}, \quad u \gt 0 \quad {\rm in} {\open R}^{3},$$
where a, b>0, 1<p<5 are constants, ϵ>0 is a parameter. Under some mild assumptions on the function V, we obtain multi-peak solutions for ϵ sufficiently small by Lyapunov–Schmidt reduction method. 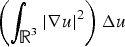Even though many results on single peak solutions to singularly perturbed Kirchhoff problems have been derived in the literature by various methods, there exist no results on multi-peak solutions before this paper, due to some difficulties caused by the nonlocal term $\left(\int_{{\open R}^{3}} \vert \nabla u \vert^{2}\right)\Delta u$. A remarkable new feature of this problem is that the corresponding unperturbed problem turns out to be a system of partial differential equations, but not a single Kirchhoff equation, which is quite different from most of the elliptic singular perturbation problems.

Keywords

Kirchhoff equationsmulti-peak positive solutionslocal Pohozaev identityLyapunov–Schmidt reduction

MSC classification

Primary: 35A01: Existence problems
Secondary: 35B25: Singular perturbations 35J20: Variational methods for second-order elliptic equations 35J60: Nonlinear elliptic equations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 149 , Issue 4 , August 2019 , pp. 1097 - 1122
Copyright
Copyright © Royal Society of Edinburgh 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Arosio, A. and Panizzi, S.. On the well-posedness of the Kirchhoff string. Trans. Amer. Math. Soc. 348 (1996), 305–330Google Scholar
2Bartsch, T. and Peng, S.. Semiclassical symmetric Schrödinger equations: existence of solutions concentrating simultaneously on several spheres. Z. Angew. Math. Phys. 58 (2007), 778–804Google Scholar
3Bernstein, S.. Sur une classe d’équations fonctionelles aux dérivées partielles. Bull. Acad. Sci. URSS. Sér. 4 (1940), 17–26Google Scholar
4Cao, D. and Peng, S.. Semi-classical bound states for Schrödinger equations with potentials vanishing or unbounded at infinity. Comm. Partial Differ. Equ. 34 (2009), 1566–1591Google Scholar
5Cao, D., Noussair, E. S. and Yan, S.. Solutions with multiple peaks for nonlinear elliptic equations. Proc. Royal Soc. Edinburgh 129 (2008), 235–264Google Scholar
6Cao, D., Li, S. and Luo, P.. Uniqueness of positive bound states with multi-bump for nonlinear Schrödinger equations. Calc. Var. Partial Differ. Equ. 54 (2015), 4037–4063Google Scholar
7D'Ancona, P. and Spagnolo, S.. Global solvability for the degenerate Kirchhoff equation with real analytic data. Invent. Math. 108 (1992), 247–262Google Scholar
8del Pino, M. and Felmer, P. L.. Local mountain passes for semilinear elliptic problems in unbounded domains. Cal. Var. PDE 4 (1996), 121–137Google Scholar
9del Pino, M. and Felmer, P. L.. Multi-peak bound states for nonlinear Schrödinger equations. Ann. Inst. H. Poincaré Anal. Non Liné aire 15 (1998), 127–149Google Scholar
10Deng, Y., Peng, S. and Shuai, W.. Existence and asymptotic behavior of nodal solutions for the Kirchhoff-type problems in ℝ3. J. Funct. Anal. 269 (2015), 3500–3527Google Scholar
11Figueiredo, G. M. and Santos Júnior, J. R.. Multiplicity and concentration behavior of positive solutions for a Schrödinger-Kirchho type problem via penalization method. ESAIM: Control, Otimiz. Calc. Variat. 20 (2014), 389–415Google Scholar
12Figueiredo, G. M., Ikoma, N. and Santos Júnior, J. R.. Existence and concentration result for the Kirchhoff type equations with general nonlinearities. Arch. Rational Mech. Anal. 213 (2014), 931–979Google Scholar
13Floer, A. and Weinstein, A.. Nonspeading wave packets for the cubic Schrödinger equation with a bounded potential. J. Funct. Anal. 69 (1986), 397–408Google Scholar
14Gui, C.. Existence of multi-bump solutions for nonlinear Schrödinger equations via variational method. Commun. Part. Differ. Equ. 21 (1996), 787–820Google Scholar
15Guo, Z.. Ground states for Kirchhoff equations without compact condition. J. Differ. Equ. 259 (2015), 2884–2902Google Scholar
16He, Y.. Concentrating bounded states for a class of singularly perturbed Kirchhoff type equations with a general nonlinearity. J. Differ. Equ. 261 (2016), 6178–6220Google Scholar
17He, Y. and Li, G.. Standing waves for a class of Kirchhoff type problems in ℝ3 involving critical Sobolev exponents. Calc. Var. Partial Differ. Equ. 54 (2015), 3067–3106Google Scholar
18He, X. M. and Zou, W. M.. Existence and concentration behavior of positive solutions for a Kirchhoff equation in ℛ3. J. Differ. Equ. 252 (2012), 1813–1834Google Scholar
19He, Y., Li, G. and Peng, S.. Concentrating bound states for Kirchhoff type problems in ℝ3 involving critical Sobolev exponents. Adv. Nonlinear Stud. 14 (2014), 483–510.Google Scholar
20Kirchhoff, G.. Mechanik (Leipzig: Teubner, 1883).Google Scholar
21Kwong, M. K.. Uniqueness of positive solutions of Δu−u+u p=0 in Rn. Arch. Rational Mech. Anal. 105 (1989), 243–266Google Scholar
22Li, G. and Ye, H.. Existence of positive ground state solutions for the nonlinear Kirchhoff type equations in ℝ3. J. Differ. Equ. 257 (2014), 566–600Google Scholar
23Li, Y., Li, F. and Shi, J.. Existence of a positive solution to Kirchhoff type problems without compactness conditions. J. Differ. Equ. 253 (2012), 2285–2294.Google Scholar
24Li, G., Luo, P., Peng, S., Wang, C. and Xiang, C.-L.. Uniqueness and Nondegeneracy of positive solutions to Kirchhoff equations and its applications in singular perturbation problems. Preprint at arXiv:1703.05459 [math.AP].Google Scholar
25Lions, J. L.. On some questions in boundary value problems of mathematical physics. In Contemporary Development in Continuum Mechanics and Partial Differential Equations, De La Penha, Guilherme M., Medeiros, Luiz Adauto J. (eds), North-Holland Math. Stud., vol. 30, pp. 284–346 (Amsterdam, New York: North-Holland, 1978).Google Scholar
26Noussair, E. S. and Yan, S.. On positive multipeak solutions of a nonlinear elliptic problem. J. London Math. Soc. (2) 62 (2000), 213–227Google Scholar
27Oh, Y. G.. Existence of semiclassical bound states of nonlinear Schrödinger equations with potentials of class (V)a. Commun. Part. Differ. Equ. 13 (1988), 1499–1519Google Scholar
28Oh, Y. G.. On positive multi-lump bound states of nonlinear Schrödinger equations under multiple well potential. Commun. Math. Phys. 131 (1990), 223–253Google Scholar
29Perera, K. and Zhang, Z.. Nontrivial solutions of Kirchhoff-type problems via the Yang index. J. Differ. Equ. 221 (2006), 246–255Google Scholar
30Pohozaev, S. I.. A certain class of quasilinear hyperbolic equations. Mat. Sb. (N.S.) 96 (1975), 152–166, 168 (in Russian)Google Scholar
31Rabinowitz, P. H.. On a class of nonlinear Schrödinger equations. Z. Angew. Math. Phys. 43 (1992), 270–291Google Scholar
32Wang, J., Tian, L., Xu, J. and Zhang, F.. Multiplicity and concentration of positive solutions for a Kirchhoff type problem with critical growth. J. Differ. Equ. 253 (2012), 2314–2351.Google Scholar