Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-12-01T01:54:01.677Z Has data issue: false hasContentIssue false
  • English
  • Français

Monotone techniques and some existence-uniqueness theorems for two point boundary value problems

Published online by Cambridge University Press:  14 November 2011

Song-Sun Lin
Song-Sun Lin
Affiliation:
Department of Applied Mathematics, National Chiao Tung University, Hsin-Chu, Taiwan 300, Republic of China
Get access Rights & Permissions [Opens in a new window]

Synopsis

In this paper we study the existence and uniqueness of the two point boundary value problems −(p(x)u′(x))′ = f(x, u(x), u′(x)), xε(0, 1), u′(0)−cu(0) = 0 = u′(1) + du(1), where ∂f/∂u is bounded. above by the least eigenvalue of associated linear problems and ∂f/∂u is bounded. By using monotone techniques to investigate the equivalent problem −(p(x)u′(x))′ + r(x)u(x) = f(x, u(x), u′(x)) + r(x)u(x) where r ε C[0, 1] we show that

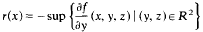
gives the optimal bounds for ∂f/∂u and ∂f/u′ when c and d are nonnegative constants.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 91 , Issue 3-4 , 1982 , pp. 265 - 275
Copyright
Copyright © Royal Society of Edinburgh 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Brown, K. J. and Lin, S. S.. Monotone techniques and semilinear elliptic boundary value problems. Proc. Roy. Soc. Edinburgh Sect. A 80 (1978), 139–149.CrossRefGoogle Scholar
2Brown, K. J. and Lin, S. S.. Periodically perturbed conservative systems and a global inverse function theorem. Nonlinear Anal, Theory, Methods & Appl. 4 (1979), 193–201.CrossRefGoogle Scholar
3Cesari, L.. Nonlinear oscillations across a point of resonance for nonselfadjoint systems. J. Differential Equations 28 (1978), 43–59.CrossRefGoogle Scholar
4Figueiredo, D. G. De. The Dirichlet problem for nonlinear elliptic equations: a Hilbert space approach. Lecture Notes in Mathematics 445, 144–165 (Springer: New York, 1974).Google Scholar
5Figueiredo, D. G. De and Gossez, J. P.. Nonlinear perturbations of a linear elliptic problem near its first eigenvalue. J. Differential Equations 30 (1978), 1–19.CrossRefGoogle Scholar
6Hess, P.. On a theorem by Landesman and Lazer. Indiana Univ. Math. J. 23 (1974), 827–829.CrossRefGoogle Scholar
7Kannan, R. and Locker, J.. On a class of nonlinear boundary value problems. J. Differential Equations 26 (1977), 1–8.CrossRefGoogle Scholar
8Kato, T.. Perturbation theory for linear operators (Berlin: Springer, 1966).Google Scholar
9Landesman, E. M. and Lazer, A. C.. Linear eigenvalues and a nonlinear boundary value problem. Pacific J. Math. 33 (1970), 331–328.CrossRefGoogle Scholar
10Landesman, E. M. and Lazer, A. C.. Nonlinear perturbations of linear elliptic boundary value problems at resonance. J. Math. Mech. 19 (1970), 609–623.Google Scholar
11Lazer, A. C. and Leach, D. E.. Bounded perturbations of forced harmonic oscillations at resonance. Ann. Mate. Pura Appl. 72 (1969), 49–68.CrossRefGoogle Scholar
12Lazer, A. C. and Sánchez, D. A.. On periodically perturbed conservative systems. Michigan Math. J. 16 (1969), 193–200.CrossRefGoogle Scholar
13. McKenna, P. J.. Nonselfadjoint semilinear problems at resonance in the alternative method. J. Differential Equations 33 (1979), 275–293.CrossRefGoogle Scholar
14Tippett, J.. An existence-uniqueness theorem for two point boundary value problems. SIAM J. Math. Anal. 5 (1974), 153–157.CrossRefGoogle Scholar
15Williams, S. A.. A sharp sufficient condition for solution of nonlinear elliptic boundary value problem. J. Differential Equations 8 (1970), 580–586.CrossRefGoogle Scholar