Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-25T17:36:40.470Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimal isometric dilations and operator models for the polydisc

Part of: Special classes of linear operators General theory of linear operators

Published online by Cambridge University Press:  26 November 2024

Sourav Pal Open the ORCID record for Sourav Pal [Opens in a new window]  and
Prajakta Sahasrabuddhe
Sourav Pal
Affiliation:
Mathematics Department, Indian Institute of Technology Bombay, Powai, Mumbai, Maharashtra, 400076, India ([email protected], [email protected]) (corresponding author)
Prajakta Sahasrabuddhe
Affiliation:
Mathematics Department, Indian Institute of Technology Bombay, Powai, Mumbai, Maharashtra, 400076, India ([email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

For commuting contractions $T_1,\dots,T_n$ acting on a Hilbert space 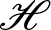$\mathscr{H}$ with 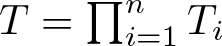$T=\prod_{i=1}^n T_i$, we find a necessary and sufficient condition such that $(T_1,\dots,T_n)$ dilates to a commuting tuple of isometries $(V_1,\dots,V_n)$ on the minimal isometric dilation space of T with 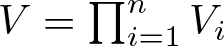$V=\prod_{i=1}^nV_i$ being the minimal isometric dilation of T. This isometric dilation provides a commutant lifting of $(T_1, \dots, T_n)$ on the minimal isometric dilation space of T. We construct both Schäffer and Sz. Nagy–Foias-type isometric dilations for $(T_1,\dots,T_n)$ on the minimal dilation spaces of T. Also, a different dilation is constructed when the product T is a 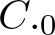$C._0$ contraction, that is, 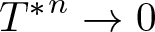${T^*}^n \rightarrow 0$ as 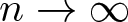$n \rightarrow \infty$. As a consequence of these dilation theorems, we obtain different functional models for $(T_1,\dots,T_n)$ in terms of multiplication operators on vectorial Hardy spaces. One notable fact about our models is that the multipliers are all analytic functions in one variable. The dilation when T is a 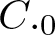$C._0$ contraction leads to a conditional factorization of T. Several examples have been constructed.

Keywords

polydisccommuting contractionsisometric dilationminimality of dilationfunctional model

MSC classification

Primary: 47A20: Dilations, extensions, compressions 47A25: Spectral sets 47A45: Canonical models for contractions and nonselfadjoint operators 47B35: Toeplitz operators, Hankel operators, Wiener-Hopf operators 47B38: Operators on function spaces (general)
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 40
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

*

Dedicated to Prof. B. V. Rajarama Bhat with deepest respect.

References

Agler, J.. The Arveson extension theorem and coanalytic models. Integ. Equ. Oper. Theory. 5 (1982), 608–631.CrossRefGoogle Scholar
Agler, J.. Hypercontractions and subnormality. J. Oper. Theory. 13 (1985), 203–217.Google Scholar
Agler, J. and McCarthy, J.. Distinguished varieties. Acta Math. 194 (2005), 133–153.CrossRefGoogle Scholar
Ando, T.. On a pair of commutative contractions. Acta Sci. Math. (Szeged). 24 (1963), 88–90.Google Scholar
Arias, A. and Popescu, G.. Noncommutative interpolation and Poisson transforms II. Houston J. Math. 25 (1999), 79–98.Google Scholar
Arias, A. and Popescu, G.. Noncommutative interpolation and Poisson transforms. Israel J. Math. 115 (2000), 205–234.CrossRefGoogle Scholar
Arveson, W.. Subalgebras of $C^*$-algebras. II. Acta Math. 128 (1972), 271–308.CrossRefGoogle Scholar
Arveson, W.. Subalgebras of $C^*$-algebras III: multivariable operator theory. Acta Math. 181 (1998), 159–228.CrossRefGoogle Scholar
Athavale, A.. Holomorphic kernels and commuting operators. Trans. Amer. Math. Soc. 304 (1987), 101–110.CrossRefGoogle Scholar
Athavale, A.. Model theory on the unit ball in $\mathbb{C}^m$. J. Oper. Theory. 27 (1992), 347–358.Google Scholar
Athavale, A.. On the intertwining of joint isometries. J. Oper. Theory. 23 (1990), 339–350.Google Scholar
Bagchi, B., Bhattacharyya, T. and Misra, G.. Some thoughts on Ando’s theorem and Parrott’s example. Linear Algebra Appl. 341 (2002), 357–367.CrossRefGoogle Scholar
Ball, J. A., Li, W. S., Timotin, D. and Trent, T. T.. A commutant lifting theorem on the polydisc. Indiana Univ. Math. J. 48 (1999), 653–675.CrossRefGoogle Scholar
Ball, J., Trent, T. and Vinnikov, V.. Interpolation and commutant lifting for multipliers on reproducing Kernel Hilbert spaces, operator theory and analysis, Oper. Theory Adv. Appl.. Vol.122, , (Birkhäuser, Basel, 2001).Google Scholar
Barik, S., Das, B. K., Haria, K. J. and Sarkar, J.. Isometric dilations and von Neumann inequality for a class of tuples in the polydisc. Trans. Amer. Math. Soc. 372 (2019), 1429–1450.CrossRefGoogle Scholar
Bercovici, H., Douglas, R. G. and Foias, C.. On the classification of multi-isometries. Acta Sci. Math. (Szeged). 72 (2006), 639–661.Google Scholar
Bercovici, H., Foias, C., Kerchy, L. and Sz.-Nagy, B.. Harmonic analysis of operators on Hilbert space, Universitext. (Springer, New York, 2010).Google Scholar
Berger, C. A., Coburn, L. A. and Lebow, A.. Representation and index theory for $C^*$-algebras generated by commuting isometries. J. Funct. Anal. 27 (1978), 51–99.CrossRefGoogle Scholar
Bhat, B. V. R., Bhattacharyya, T. and Dey, S.. Standard noncommuting and commuting dilations of commuting tuples. Trans. Amer. Math. Soc. 356 (2004), 1551–1568.CrossRefGoogle Scholar
Bhattacharyya, T.. Dilation of contractive tuples: a survey. Surveys in analysis and operator theory (Canberra, 2001), Proc. Centre Math. Appl. Austral. Nat. Univ., Vol. 40, (Austral. Nat. Univ., Canberra, 2002).Google Scholar
Bhattacharyya, T. and Pal, S.. A functional model for pure Γ-contractions. J. Oper. Theory. 71 (2014), 327–339.CrossRefGoogle Scholar
Binding, P., Farenick, D. R. and Li, C. -K.. A dilation and norm in several variable operator theory. Canad. J. Math. 47 (1995), 449–461.CrossRefGoogle Scholar
Brehmer, S.. Über vetauschbare Kontraktionen des Hilbertschen Raumes. Acta Sci. Math. (Szeged). 22 (1961), 106–111.Google Scholar
Bunce, J. W.. Models for n-tuples of noncommuting operators. J. Funct. Anal. 57 (1984), 21–30.CrossRefGoogle Scholar
Choi, M. D. and Li, C. K.. Constrained unitary dilations and numerical ranges. J. Oper. Theory. 46 (2001), 435–447.Google Scholar
Crabb, M. and Davie, A.. von Nemann’s inequality for Hilbert space operators. Bull. London Math. Soc. 7 (1975), 49–50.CrossRefGoogle Scholar
Curto, R. and Vasilescu, F. H.. Standard operator models in the polydisc. Indiana Univ. Math. J. 42 (1993), 791–810.CrossRefGoogle Scholar
Curto, R. and Vasilescu, F. H.. Standard operator models in the polydisc II. Indiana Univ. Math. J. 44 (1995), 727–746.CrossRefGoogle Scholar
Das, B. K. and Sarkar, J.. Ando dilations, von Neumann inequality, and distinguished varieties. J. Funct. Anal. 272 (2017), 2114–2131.CrossRefGoogle Scholar
Davis, C.. Some dilation and representation theorems, Proceedings of the Second International Symposium in West Africa on Functional Analysis and its Applications (Kumasi, Ghana, 1979), .Google Scholar
Dey, S.. Standard commuting dilations and liftings. Colloq. Math. 126 (2012), 87–94.CrossRefGoogle Scholar
Douglas, R. G.. Structure theory for operators I. J. Reine Angew. Math. 232 (1968), 180–193.Google Scholar
Drury, S.. A generalization of von Neumann’s inequality to the complex ball. Proc. Amer. Math. Soc. 68 (1978), 300–304.Google Scholar
Drury, S.. Remarks on von Neumann’s inequality. Banach spaces, harmonic analysis and probability theory, Lecture Notes in Math., Vol.995, (Springer, Berlin, 1983).Google Scholar
Frazho, A. E.. Models for non-commuting operators. J. Funct. Anal. 48 (1982), 1–11.CrossRefGoogle Scholar
Grinshpan, A., Kaliuzhnyi-Verbovetskyi, D. S., Vinnikov, V. and Woerdeman, H. J.. Classes of tuples of commuting contractions satisfying the multivariable von Neumann inequality. J. Funct. Anal. 256 (2009), 3035–3054.CrossRefGoogle Scholar
Halmos, P. R.. Normal dilations and extensions of operators. Summa Brasil. Math. 2 (1950), 125–134.Google Scholar
Halperin, I.. Sz.-Nagy-Brehmer dilations. Acta Sci. Math. (Szeged). 23 (1962), 279–289.Google Scholar
Halperin, I.. Intrinsic description of the Sz.-Nagy–Brehmer unitary dilation. Studia Math. 22 (1962/1963), 211–219.CrossRefGoogle Scholar
Holbrook, J. A.. Schur norms and the multivariate von Neumann inequality. Recent Advances in Operator Theory and Related Topics (Szeged, 1999) Oper. Theory Adv. Appl., Vol.127, (Birkhäuser, Basel, 2001).Google Scholar
Julia, G.. Les projections des systèmes orthonormaux de l’espace Hilbertien. C. R. Acad. Sci. Paris. 218 (1944), 892–895.Google Scholar
Julia, G.. Les projections des systèmes orthonormaux de l’espace Hilbertien et les opérateurs bornés. C. R. Acad. Sci. Paris. 219 (1944), 8–11.Google Scholar
Julia, G.. Sur la représentation analytique des opérateurs bornés ou fermés de l’espace Hilbertien. C. R. Acad. Sci. Paris. 219 (1944), 225–227.Google Scholar
Knese, G.. The von Neumann inequality for $3\times 3$ matrices. Bull. London Math. Soc. 48 (2016), 53–57.CrossRefGoogle Scholar
Levy, E. and Moshe Shalit, O.. Dilation theory in finite dimensions: the possible, the impossible and the unknown. Rocky Mountain J. Math. 44 (2014), 203–221.CrossRefGoogle Scholar
Müller, V. and Vasilescu, F. H.. Standard models for some commuting multishifts. Proc. Amer. Math. Soc. 117 (1993), 979–989.CrossRefGoogle Scholar
McCarthy, J. and Shalit, O.. Unitary n-dilations for tuples of commuting matrices. Proc. Amer. Math. Soc. 141 (2013), 563–571.CrossRefGoogle Scholar
Parrott, S.. Unitary dilations for commuting contractions. Pacific J. Math. 34 (1970), 481–490.CrossRefGoogle Scholar
Popescu, G.. Isometric dilations for infinite sequences of noncommuting operators. Trans. Amer. Math. Soc. 316 (1989), 523–536.CrossRefGoogle Scholar
Popescu, G.. Models for infinite sequences of noncommuting operators. Acta Sci. Math. (Szeged). 53 (1989), 355–368.Google Scholar
Popescu, G.. Characteristic functions for infinite sequences of noncommuting operators. J. Oper. Theory. 22 (1989), 51–71.Google Scholar
Popescu, G.. Poisson transforms on some -algebras generated by isometries. J. Funct. Anal. 161 (1999), 27–61.CrossRefGoogle Scholar
Popescu, G.. Curvature invariant for Hilbert modules over free semigroup algebras. Adv. Math. 158 (2001), 264–309.CrossRefGoogle Scholar
Sau, H.. Andó dilations for a pair of commuting contractions: two explicit constructions and functional models. https://arxiv.org/abs/1710.11368.Google Scholar
Shalit, O. M.. Dilation theory: a guided tour. Operator theory, functional analysis and applications Oper. Theory Adv. Appl., Vol.282, (Birkhäuser/Springer, Cham, 2021).Google Scholar
Stochel, J. and Szafraniec, F. H.. Unitary dilation of several contractions. Oper. Theory Adv. Appl. 127 (2001), 585–598.Google Scholar
Sz.-Nagy, B.. Sur les contractions de I’espace de Hilbert. Acta Sci. Math. (Szeged). 15 (1953), 87–92.Google Scholar
Sz.-Nagy, B.. Transformations of Hilbert space, positive definite functions on a semigroup. Usp. Mat. Nauk. 11 (1956), 173–182.Google Scholar
Timotin, D.. Regular dilations and models for multicontractions. Indiana Univ. Math. J. 47 (1998), 671–684.CrossRefGoogle Scholar
Varopoulos, N.. On an inequality of von Neumann and an application of the metric theory of tensor products to operator theory. J. Funct. Anal. 16 (1974), 83–100.CrossRefGoogle Scholar
Vasilescu, F. H.. An operator-valued Poisson kernel. J. Funct. Anal. 110 (1992), 47–72.CrossRefGoogle Scholar
von Neumann, J.. Eine Spektraltheorie für allgemeine Operatoren eines unitären Raumes. Math. Nachr. 4 (1951), 258–281.CrossRefGoogle Scholar