Published online by Cambridge University Press: 13 January 2020
This paper is concerned with the following nonlinear Schrödinger system in 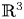 ${\mathbb R}^3$
${\mathbb R}^3$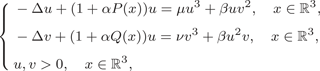 $$\left\{ {\beging{matrix}{ {-\Delta u + (1 + \alpha P(x))u = \mu u^3 + \beta uv^2,} \hfill & {x\in {\open R}^3,} \hfill \cr {-\Delta v + (1 + \alpha Q(x))u = \nu v^3 + \beta u^2v,} \hfill & {x\in {\open R}^3,} \hfill \cr {u,v > 0,} \hfill & {x\in {\open R}^3,} \hfill \cr } } \right.$$
$$\left\{ {\beging{matrix}{ {-\Delta u + (1 + \alpha P(x))u = \mu u^3 + \beta uv^2,} \hfill & {x\in {\open R}^3,} \hfill \cr {-\Delta v + (1 + \alpha Q(x))u = \nu v^3 + \beta u^2v,} \hfill & {x\in {\open R}^3,} \hfill \cr {u,v > 0,} \hfill & {x\in {\open R}^3,} \hfill \cr } } \right.$$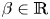 $\beta \in {\mathbb R}$ is a coupling constant,
$\beta \in {\mathbb R}$ is a coupling constant, 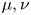 $\mu ,\nu $ are positive constants, P,Q are weight functions decaying exponentially to zero at infinity, α can be regarded as a parameter. This type of system arises, in particular, in models in Bose–Einstein condensates theory and Kerr-like photo refractive media.
$\mu ,\nu $ are positive constants, P,Q are weight functions decaying exponentially to zero at infinity, α can be regarded as a parameter. This type of system arises, in particular, in models in Bose–Einstein condensates theory and Kerr-like photo refractive media.
We prove that, for any positive integer k > 1, there exists a suitable range of α such that the above problem has a non-radial positive solution with exactly k maximum points which tend to infinity as 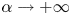 $\alpha \to +\infty $ (or
$\alpha \to +\infty $ (or 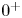 $0^+$). Moreover, we also construct prescribed number of sign-changing solutions.
$0^+$). Moreover, we also construct prescribed number of sign-changing solutions.