Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kato, Tosio
1984.
Nonselfadjoint Schrödinger operators with singular first-order coefficients.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 96,
Issue. 3-4,
p.
323.
Miyajima, Shizuo
1986.
Aspects of Positivity in Functional Analysis, Proceedings of the Conference held on the Occasion of H.H. Schaefer's 60th Birthday.
Vol. 122,
Issue. ,
p.
241.
Kumar, Rajiv
and
Das, Purna C.
1991.
Perturbation of m-accretive operators in banach spaces.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 17,
Issue. 2,
p.
161.
Hieber, Matthias
1994.
Spectral theory of positive semigroups generated by differential operators.
Archiv der Mathematik,
Vol. 63,
Issue. 4,
p.
333.
Okazawa, Noboru
and
Sobajima, Motohiro
2014.
New Prospects in Direct, Inverse and Control Problems for Evolution Equations.
Vol. 10,
Issue. ,
p.
401.
Challifour, John L.
and
Timko, Edward J.
2016.
Canonical quantization of lattice Higgs-Yang-Mills fields: Krein essential selfadjointness of the Hamiltonian.
Journal of Mathematical Physics,
Vol. 57,
Issue. 6,
Do, Tan Duc
and
ter Elst, A. F. M.
2016.
One-dimensional degenerate elliptic operators on $$L_{\!p}$$ L p -spaces with complex coefficients.
Semigroup Forum,
Vol. 92,
Issue. 3,
p.
559.
Do, Tan Duc
2019.
Core properties for degenerate elliptic operators with complex bounded coefficients.
Journal of Mathematical Analysis and Applications,
Vol. 479,
Issue. 1,
p.
817.
Do, Tan Duc
2021.
On sectoriality of degenerate elliptic operators.
Proceedings of the Edinburgh Mathematical Society,
Vol. 64,
Issue. 3,
p.
689.
Do, Tan Duc
and
Elst, A. F. M. ter
2023.
From Complex Analysis to Operator Theory: A Panorama.
Vol. 291,
Issue. ,
p.
405.
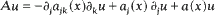
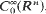 , the minimal realization of –A, is essentially quasi-m-dispersive in Lp(Rn), (hence that the minimal realization of +A is quasi-m-accretive) and that its closure coincides with the maximal realization of –A.
, the minimal realization of –A, is essentially quasi-m-dispersive in Lp(Rn), (hence that the minimal realization of +A is quasi-m-accretive) and that its closure coincides with the maximal realization of –A.