Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T12:23:48.393Z Has data issue: false hasContentIssue false
  • English
  • Français

Lorentz and Gale–Ryser theorems on general measure spaces

Part of: Classical measure theory Linear function spaces and their duals Inequalities

Published online by Cambridge University Press:  09 August 2021

Santiago Boza Open the ORCID record for Santiago Boza [Opens in a new window] ,
Martin Křepela Open the ORCID record for Martin Křepela [Opens in a new window]  and
Javier Soria Open the ORCID record for Javier Soria [Opens in a new window]
Santiago Boza
Affiliation:
Department of Mathematics, EETAC, Polytechnical University of Catalonia, 08860 Castelldefels, Spain [email protected]
Martin Křepela
Affiliation:
Faculty of Electrical Engineering, Department of Mathematics, Czech Technical University in Prague, Technická 2, 166 27 Praha 6, Czech Republic [email protected]
Javier Soria
Affiliation:
Interdisciplinary Mathematics Institute (IMI), Department of Analysis and Applied Mathematics, Complutense University of Madrid, 28040 Madrid, Spain [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Based on the Gale–Ryser theorem [2, 6], for the existence of suitable 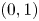$(0,1)$-matrices for different partitions of a natural number, we revisit the classical result of Lorentz [4] regarding the characterization of a plane measurable set, in terms of its cross-sections, and extend it to general measure spaces.

Keywords

Cross-sectionsNonincreasing rearrangementHardy-Littlewood-Pólya relation

MSC classification

Primary: 26D15: Inequalities for sums, series and integrals
Secondary: 28A35: Measures and integrals in product spaces 46E30: Spaces of measurable functions ($L^p$-spaces, Orlicz spaces, Köthe function spaces, Lorentz spaces, rearrangement invariant spaces, ideal spaces, etc.)
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 4 , August 2022 , pp. 857 - 878
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bennett, C. and Sharpley, R.. Interpolation of Operators (Boston: Academic Press, 1988).Google Scholar
Gale, D.. A theorem on flows in networks. Pacific J. Math. 7 (1957), 1073–1082.CrossRefGoogle Scholar
Krause, M.. A simple proof of the Gale-Ryser theorem. Amer. Math. Monthly 103 (1996), 335–337.CrossRefGoogle Scholar
Lorentz, G. G.. A problem on plane measures. Amer. J. Math. 71 (1949), 417–426.CrossRefGoogle Scholar
Ryff, J. V.. Measure preserving transformations and rearrangements. J. Math. Anal. Appl. 31 (1970), 449–458.CrossRefGoogle Scholar
Ryser, H. J.. Combinatorial properties of matrices of zeros and ones. Can. J. Math. 9 (1957), 371–377.CrossRefGoogle Scholar
Sierksma, G. and Hoogeveen, H.. Seven criteria for integer sequences being graphic. J. Graph Theory 15 (1991), 223–231.CrossRefGoogle Scholar
Sierpiński, W.. Sur les fonctions d'ensemble additives et continues. Fund. Math. 3 (1922), 240–246.CrossRefGoogle Scholar