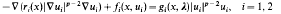Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Huang, Yin Xi
and
So, Joseph W.-H.
1995.
On Bifurcation and Existence of Positive Solutions for a Certain $p$-Laplacian System.
Rocky Mountain Journal of Mathematics,
Vol. 25,
Issue. 1,