Let f(·, λ) : R→R be given so that f(0, λ) = 0 and f(x, λ) = (1 + λ)x + ax2 + bx3 + o(x3) as x → 0. We characterize those small values of ε > 0 and λ ∈ R for which there are periodic solutions of periods approximately 1/k with k ∈ N of the delay equations 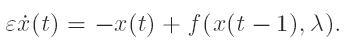When a = 0, these periodic solutions approach square waves if b < 0 or pulses if b > 0 as ε → 0. These results are similar to those obtained by Chow et al. and Hale and Huang, where the case of f(x, λ) = −(1 + λ)x + ax2 + bx3 + o(x3) as x → 0 is considered. However, when a ≠ 0, all these periodic solutions approach pulses as ε → 0; an interesting phenomenon that cannot happen in the case considered by Chow et al. and Hale and Huang.