Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-19T05:56:48.605Z Has data issue: false hasContentIssue false
  • English
  • Français

The limit of the anisotropic double-obstacle Allen–Cahn equation

Published online by Cambridge University Press:  14 November 2011

Charles M. Elliott  and
Reiner Schätzle
Charles M. Elliott
Affiliation:
Centre for Mathematical Analysis and its Applications, School of Mathematical Sciences, University of Sussex, Falmer, Brighton BN1 9QH, U.K. e-mail: [email protected]
Reiner Schätzle
Affiliation:
Universität Bonn, Institut für Angewandte Mathematik, Wegelerstraße 6, D-53115 Bonn, Germany e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we prove that solutions of the anisotropic Allen–Cahn equation in doubleobstacle form

where A is a strictly convex function, homogeneous of degree two, converge to an anisotropic mean-curvature flow

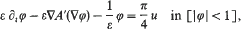
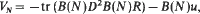
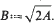when this equation admits a smooth solution in ℝn. Here VN and R respectively denote the normal velocity and the second fundamental form of the interface, and More precisely, we show that the Hausdorff-distance between the zero-level set of φ and the interface of the above anisotropic mean-curvature flow is of order O(ε2).

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 126 , Issue 6 , 1996 , pp. 1217 - 1234
Copyright
Copyright © Royal Society of Edinburgh 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Allen, S. and Cahn, J.. A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsing. Ada Metall. 27 (1979), 1084–95.CrossRefGoogle Scholar
2Blowey, J. F. and Elliott, C. M.. Curvature dependent phase boundary motion and parabolic obstacle problems. In Proc. IMA Workshop on Degenerate Diffusion, eds Ni, W., Peletier, L. and Vasquez, J. L.), IMA 47, 19–60 (Berlin: Springer, 1993).CrossRefGoogle Scholar
3Caginalp, G.. An analysis of a phase-field model of a free boundary. Arch. Rational Mech. Anal. 92 (1986), 205–45.CrossRefGoogle Scholar
4Chen, X.. Generation and propagation of interface in reaction-diffusion equations. J. Differential Equations 96 (1992), 116–41.CrossRefGoogle Scholar
5Chen, X. and Elliott, C. M.. Asymptotics for a parabolic double obstacle problem. Proc. Roy. Soc. London Ser. A 444 (1994), 429–45.Google Scholar
6Mottoni, P. de and Schatzmann, M.. Evolution geometrique d'interfaces. C. R. Acad. Sci. Paris Ser. 1 Math. 309 (1989), 453–8.Google Scholar
7Evans, L. C., Soner, H. M. and Souganidis, P. E.. Phase transitions and generalized motion by mean curvature. Comm. Pure Appl. Math. 45 (1992), 1097–123.CrossRefGoogle Scholar
8McFadden, G. B., Wheeler, A. A., Braun, R. J, Coriell, S. R. and Sekerka, R. F.. Phase-field models for anisotropic interfaces. Phys. Rev. E 48 (1993), 2016–24.CrossRefGoogle ScholarPubMed
9Modica, L.. The gradient theory of phase transitions and the minimal interface criterion. Arch. Rational Mech. Anal. 98 (1987), 123–42.CrossRefGoogle Scholar
10Nochetto, R. H., Paolini, M. and Verdi, C.. Sharp error analysis for curvature dependent evolving fronts. Math. Models Methods Appl. Sci. 3 (1993), 771–23.CrossRefGoogle Scholar
11Nochetto, R. H. and Verdi, C.. Convergence of double obstacle problems to the geometric motions of fronts (Quaderno 39, Universita degli Studi di Milano, 1994).Google Scholar
12Taylor, J. E. and Cahn, J. W.. Linking anisotropic sharp and diffuse surface motion laws via gradient flows. J. Statist. Phys. 77 (1993), 183–97.CrossRefGoogle Scholar
13Wheeler, A. A. and McFadden, G. B.. A ξ-vector formulation of anisotropic phase-field models: 3-D asymptotics (Univeristy of Bristol Mathematics Research Report, AM-94–05, Bristol, 1994).Google Scholar