Article contents
Left approximate identities in algebras of compact operators on Banach spaces
Published online by Cambridge University Press: 14 November 2011
Synopsis
We study the existence of left approximate units, left approximate identities and bounded left approximate identities in the algebras 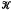 (X)of all compact operators on a Banach space X and ℱ(X)− of all operators uniformly approximable by finite rank operators. In the case of bounded left approximate identities, necessary and sufficient conditions on X are obtained. In the other cases, sufficient conditions are obtained, together with an example of non-existence using a space constructed by Szankowski. The possibility of the sufficient conditions being also necessary depends on the question of whether every compact set is contained in the closure of the image of the unit ball under an operator in
(X)of all compact operators on a Banach space X and ℱ(X)− of all operators uniformly approximable by finite rank operators. In the case of bounded left approximate identities, necessary and sufficient conditions on X are obtained. In the other cases, sufficient conditions are obtained, together with an example of non-existence using a space constructed by Szankowski. The possibility of the sufficient conditions being also necessary depends on the question of whether every compact set is contained in the closure of the image of the unit ball under an operator in 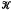 (X)(or ℱ(X)−). Sufficient conditions on X are obtained for this to be true, but it is conjectured that the answer for general X is negative.
(X)(or ℱ(X)−). Sufficient conditions on X are obtained for this to be true, but it is conjectured that the answer for general X is negative.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 104 , Issue 1-2 , 1986 , pp. 169 - 175
- Copyright
- Copyright © Royal Society of Edinburgh 1986
References
- 8
- Cited by


