Published online by Cambridge University Press: 14 November 2011
The paper provides an example of an integral functional in more than two dimensions, with a symmetric and positively defined quadratic integrand q, exhibiting the Lavrentieff phenomenon on a ball B and on a linear boundary datum u0, i.e. for which
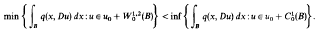
The example is also utilised to discuss nonidentity between some relaxation procedures for a quadratic integral functional and to provide a weighted Sobolev space in the Hilbert case in which smooth functions are not dense.