Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Yokota, Tomomi
2003.
Nonlinear Analysis and Applications: To V. Lakshmikantham on his 80th Birthday.
p.
939.
Hayashi, Nakao
Kaikina, Elena I.
and
Naumkin, Pavel I.
2003.
Global existence and time decay of small solutions to the landau-ginzburg type equations.
Journal d'Analyse Mathématique,
Vol. 90,
Issue. 1,
p.
141.
HAYASHI, NAKAO
KAIKINA, ELENA I.
and
NAUMKIN, PAVEL I.
2003.
LANDAU–GINZBURG TYPE EQUATIONS IN THE SUBCRITICAL CASE.
Communications in Contemporary Mathematics,
Vol. 05,
Issue. 01,
p.
127.
Hayashi, Nakao
Kaikina, Elena I.
and
Naumkin, Pavel I.
2004.
Damped wave equation in the subcritical case.
Journal of Differential Equations,
Vol. 207,
Issue. 1,
p.
161.
Hayashi, Nakao
and
Naumkin †, Pavel I.
2004.
On the asymptotics for cubic nonlinear Schrödinger equations.
Complex Variables, Theory and Application: An International Journal,
Vol. 49,
Issue. 5,
p.
339.
Kaikina, Elena I.
Naumkin, Pavel I.
and
Sánchez-Suárez, Isahi
2004.
Nonlinear nonlocal Schrödinger type equations on a segment.
SUT Journal of Mathematics,
Vol. 40,
Issue. 1,
Kaikina, Elena I.
2004.
Nonlinear nonlocal Whitham equation on a segment.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 59,
Issue. 1-2,
p.
55.
Hayashi, Nakao
Ito, Naoko
Kaikina, Elena I.
and
Naumkin, Pavel I.
2004.
Large Time Behavior of Small Solutions to Dirichlet Problem for Landau-Ginzburg Type Equations.
Funkcialaj Ekvacioj,
Vol. 47,
Issue. 3,
p.
479.
Kaikina, Elena I.
2005.
Subcritical nonlinear nonlocal equations on a half-line.
Journal of Mathematical Analysis and Applications,
Vol. 305,
Issue. 1,
p.
316.
Hayashi, Nakao
Ito, Naoko
Kaikina, Elena I.
and
Naumkin, Pavel I.
2005.
Large time decay of solutions to Burgers type equations.
Applicable Analysis,
Vol. 84,
Issue. 10,
p.
1005.
Hayashi, Nakao
Kaikina, Elena
and
Naumkin, Pavel
2005.
Damped wave equation with a critical nonlinearity.
Transactions of the American Mathematical Society,
Vol. 358,
Issue. 3,
p.
1165.
Hayashi, Nakao
Kaikina, Elena I.
and
Naumkin, Pavel I.
2005.
Asymptotics of solutions for sub critical non‐convective type equations.
Mathematical Methods in the Applied Sciences,
Vol. 28,
Issue. 3,
p.
275.
Kaikina, Elena I.
2006.
Subcritical Kuramoto–Sivashinsky-type equation on a half-line.
Journal of Differential Equations,
Vol. 220,
Issue. 2,
p.
279.
Hayashi, Nakao
and
Naumkin, Pavel I.
2006.
Asymptotics for the Korteweg–de Vries–Burgers Equation.
Acta Mathematica Sinica, English Series,
Vol. 22,
Issue. 5,
p.
1441.
Hayashi, Nakao
and
Kaikina, Elena I.
2006.
Neumann problem for the Korteweg–de Vries equation.
Journal of Differential Equations,
Vol. 225,
Issue. 1,
p.
168.
Kaikina, Elena I.
2006.
Critical convective‐type equations on ahalf‐line.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2006,
Issue. 1,
Hayashi, Nakao
Kaikina, Elena I.
and
Naumkin, Pavel I.
2006.
Asymptotics for critical Rosenau type equations with nonconvective nonlinearites on a half-line.
Complex Variables and Elliptic Equations,
Vol. 51,
Issue. 12,
p.
1153.
Hayashi, Nakao
Kaikina, Elena I.
and
Naumkin, Pavel I.
2007.
Asymptotics in the critical case for Whitham type equations.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 67,
Issue. 10,
p.
2914.
Hayashi, Nakao
Kaikina, Elena I.
and
Naumkin, Pavel I.
2007.
Subcritical nonlinear heat equation.
Journal of Differential Equations,
Vol. 238,
Issue. 2,
p.
366.
Kaikina, E. I.
Naumkin, P. I.
and
Shishmarev, I. A.
2008.
Asymptotic behavior of solutions to a boundary value problem for a nonlinear equation with a fractional derivative.
Doklady Mathematics,
Vol. 78,
Issue. 1,
p.
485.
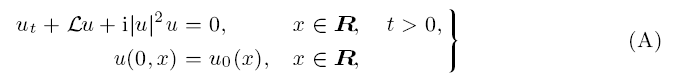 where L is a linear pseudodifferential operator with dissipative symbol ReL(ξ) ≥ C1|ξ|2/(1 + ξ2) and |L′(ξ)| ≤ C2(|ξ|+ |ξ|n) for all ξ ∈ R. Here, C1, C2 > 0, n ≥ 1. Moreover, we assume that L(ξ) = αξ2 + O(|ξ|2+γ) for all |ξ| < 1, where γ > 0, Re α > 0, Im α ≥ 0. When L(ξ) = αξ2, equation (A) is the nonlinear Schrödinger equation with dissipation ut − αuxx + i|u|2u = 0. Our purpose is to prove that solutions of (A) satisfy the time decay estimate
where L is a linear pseudodifferential operator with dissipative symbol ReL(ξ) ≥ C1|ξ|2/(1 + ξ2) and |L′(ξ)| ≤ C2(|ξ|+ |ξ|n) for all ξ ∈ R. Here, C1, C2 > 0, n ≥ 1. Moreover, we assume that L(ξ) = αξ2 + O(|ξ|2+γ) for all |ξ| < 1, where γ > 0, Re α > 0, Im α ≥ 0. When L(ξ) = αξ2, equation (A) is the nonlinear Schrödinger equation with dissipation ut − αuxx + i|u|2u = 0. Our purpose is to prove that solutions of (A) satisfy the time decay estimate
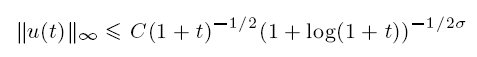 under the conditions that u0 ∈ Hn,0 ∩ H0,1 have the mean value
under the conditions that u0 ∈ Hn,0 ∩ H0,1 have the mean value
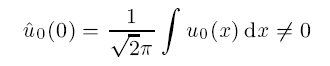 and the norm ‖u0‖Hn,0 + ‖u0‖H0,1 = ε is sufficiently small, where σ = 1 if Im α > 0 and σ = 2 if Im α = 0, and
and the norm ‖u0‖Hn,0 + ‖u0‖H0,1 = ε is sufficiently small, where σ = 1 if Im α > 0 and σ = 2 if Im α = 0, and
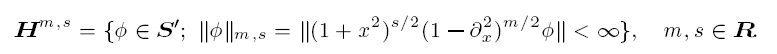 Therefore, equation (A) is considered as a critical case for the large-time asymptotic behaviour because the solutions of the Cauchy problem for the equation ut − αuxx + i|u|p−1u = 0, with p > 3 have the same time decay estimate ‖u‖L∞ = O(t−½) as that of solutions to the linear equation. On the other hand, note that solutions of the Cauchy problem (A) have an additional logarithmic time decay. Our strategy of the proof of the large-time asymptotics of solutions is to translate (A) to another nonlinear equation in which the mean value of the nonlinearity is zero for all time.
Therefore, equation (A) is considered as a critical case for the large-time asymptotic behaviour because the solutions of the Cauchy problem for the equation ut − αuxx + i|u|p−1u = 0, with p > 3 have the same time decay estimate ‖u‖L∞ = O(t−½) as that of solutions to the linear equation. On the other hand, note that solutions of the Cauchy problem (A) have an additional logarithmic time decay. Our strategy of the proof of the large-time asymptotics of solutions is to translate (A) to another nonlinear equation in which the mean value of the nonlinearity is zero for all time.