Article contents
Large-time behaviour of solutions of a reaction–diffusion equation
Published online by Cambridge University Press: 14 November 2011
Abstract
We investigate the large-time behaviour of the solutions u = u(x, t) to the one-dimensional nonlinear heat equation with reaction
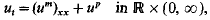
with exponents m > 1,p < 1. The initial function u(x, 0) is assumed to be measurable and nonnegative. In the case m + p ≧ 2 where the initial value does not uniquely determine the solution, we also fix the positivity set of the solution u(x, t) if the support of u(x, 0) is not the whole line ℝ, i.e. u(x, t) > 0 if and only if −s1(t) <x<s2(t), t ≧ 0, where 0≦si(t)≦∞ for t ≧ 0, i = 1, 2 are lower semicontinuous given functions. We prove that u converges to a self-similar function which depends only on the behaviour of u(x, 0) for |x| large or si(t) for t large. We classify the set of self-similar solutions and study the equation satisfied by their interfaces.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 124 , Issue 2 , 1994 , pp. 389 - 398
- Copyright
- Copyright © Royal Society of Edinburgh 1994
References
- 6
- Cited by


