Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-25T05:53:47.183Z Has data issue: false hasContentIssue false
  • English
  • Français

Instability of standing waves for fractional NLS with combined nonlinearities

Part of: Partial differential equations Equations of mathematical physics and other areas of application Miscellaneous topics - Partial differential equations

Published online by Cambridge University Press:  27 November 2024

Zaizheng Li ,
Haijun Luo  and
Zhitao Zhang
Zaizheng Li
Affiliation:
School of Mathematical Sciences, Hebei Center for Applied Mathematics, Hebei Normal University, Shijiazhuang 050024, Hebei, China ([email protected])
Haijun Luo
Affiliation:
School of Mathematics, Hunan Provincial Key Laboratory of Intelligent Information, Processing and Applied Mathematics, Hunan University, Changsha 410082, Hunan, China ([email protected]) (corresponding author)
Zhitao Zhang
Affiliation:
HLM, Academy of Mathematics and Systems Science, The Chinese Academy of Sciences, Beijing 100190, China School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the existence and strong instability of standing wave solutions for the fractional nonlinear Schrödinger equation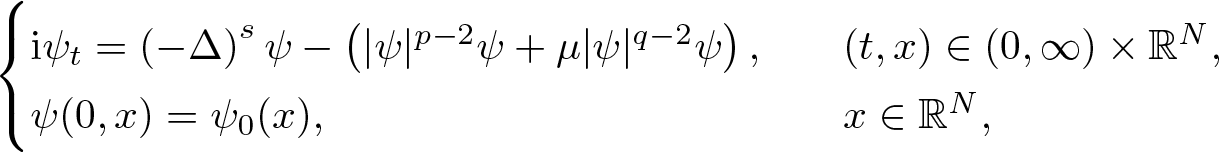

\begin{equation*}\begin{cases}\mathrm{i} \psi_{t}=\left(-\Delta\right)^s \psi-\left(|\psi|^{p-2}\psi+\mu|\psi|^{q-2}\psi\right), & \quad(t,x)\in(0,\infty)\times\mathbb{R}^N,\\\psi(0,x)=\psi_0(x),&\quad x\in\mathbb{R}^N,\end{cases}\end{equation*}

where 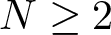$N\geq2$, 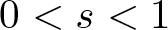$0 \lt s \lt 1$, 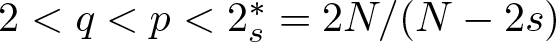$2 \lt q \lt p \lt 2_s^*=2N/(N-2s)$, and 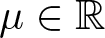$\mu\in\mathbb{R}$. The primary challenge lies in the inhomogeneity of the nonlinearity.We deal with the following three cases: (i) for $2 \lt q \lt p \lt 2+4s/N$ and µ < 0, there exists a threshold mass a0 for the existence of the least energy normalized solution; (ii) for $2+4s/N \lt q \lt p \lt 2_s^*$ and µ > 0, we reveal the existence of the ground state solution, explore the strong instability of standing waves, and provide a blow-up criterion; (iii) for 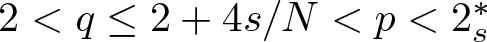$2 \lt q\leq2+4s/N \lt p \lt 2_s^*$ and µ < 0, the strong instability of standing wave solutions is demonstrated. These findings are illuminated through variational characterizations, the profile decomposition, and the virial estimate.

Keywords

fractional NLSinstabilitystanding wavevariational characterizationground state solution

MSC classification

Primary: 35R11: Fractional partial differential equations
Secondary: 35B35: Stability 35Q55: NLS-like equations (nonlinear Schrödinger)
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 29
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Almgren, F. J. Jr and Lieb, E. H.. Symmetric decreasing rearrangement is sometimes continuous. J. Amer. Math. Soc. 2 (1989), 683–773.CrossRefGoogle Scholar
Applebaum, D.. Lévy Processes and Stochastic Calculus, 2nd ed. Cambridge Studies in Advanced Mathematics. Vol.116, (Cambridge University Press, Cambridge, 2009).CrossRefGoogle Scholar
Bartsch, T. and de Valeriola, S.. Normalized solutions of nonlinear Schrödinger equations. Arch. Math. (Basel). 100 (2013), 75–83.CrossRefGoogle Scholar
Berestycki, H. and Cazenave, T.. Instabilité des états stationnaires dans les équations de Schrödinger et de Klein-Gordon non linéaires. (French) [Instability of stationary states in nonlinear Schrödinger and Klein-Gordon equations]. C. R. Acad. Sci. Paris Sér. I Math. 293 (1981), 489–492.Google Scholar
Bonheure, D., Casteras, J. -B., Gou, T., and Jeanjean, L.. Strong instability of ground states to a fourth order Schrödinger equation. Int. Math. Res. Not. IMRN. 2019 (2019), 5299–5315.CrossRefGoogle Scholar
Boulenger, T., Himmelsbach, D. and Lenzmann, E.. Blowup for fractional NLS. J. Funct. Anal. 271 (2016), 2569–2603.CrossRefGoogle Scholar
Cazenave, T. and Lions, P. -L.. Orbital stability of standing waves for some nonlinear Schrödinger equations. Comm. Math. Phys. 85 (1982), 549–561.CrossRefGoogle Scholar
Chang, X. and Wang, Z. -Q.. Ground state of scalar field equations involving a fractional Laplacian with general nonlinearity. Nonlinearity 26 (2013), 479–494.CrossRefGoogle Scholar
Chen, W., Li, C. and Li, Y.. A direct method of moving planes for the fractional Laplacian. Adv. Math. 308 (2017), 404–437.CrossRefGoogle Scholar
Colorado, E. and Ortega, A.. Nonlinear fractional Schrödinger equations coupled by power–type nonlinearities. Adv. Differ. Equ. 28 (2023), 113–142.Google Scholar
Di Nezza, E., Palatucci, G. and Valdinoci, E.. Hitchhiker’s guide to the fractional Sobolev spaces. Bull. Sci. Math. 136 (2012), 521–573.CrossRefGoogle Scholar
Dinh, V.. On instability of standing waves for the mass-supercritical fractional nonlinear Schrödinger equation. Z. Angew. Math. Phys. 70 (2019), .CrossRefGoogle Scholar
Dinh, V. and Feng, B.. On fractional nonlinear Schrödinger equation with combined power-type nonlinearities. Discrete Contin. Dyn. Syst. 39 (2019), 4565–4612.CrossRefGoogle Scholar
Felmer, P., Quaas, A. and Tan, J.. Positive solutions of the nonlinear Schrödinger equation with the fractional Laplacian. Proc. Roy. Soc. Edinb. A 142 (2012), 1237–1262.CrossRefGoogle Scholar
Feng, B., Ren, J. and Wang, Q.. Existence and instability of normalized standing waves for the fractional Schrödinger equations in the L 2-supercritical case. J. Math. Phys. 61 (2020), .CrossRefGoogle Scholar
Feng, B. and Zhu, S.. Stability and instability of standing waves for the fractional nonlinear Schrödinger equations. J. Differ. Equ. 292 (2021), 287–324.CrossRefGoogle Scholar
Frank, R. L., Lenzmann, E. and Silvestre, L.. Uniqueness of radial solutions for the fractional Laplacian. Comm. Pure Appl. Math. 69 (2016), 1671–1726.CrossRefGoogle Scholar
Gou, T. and Zhang, Z.. Normalized solutions to the Chern-Simons-Schrödinger system. J. Funct. Anal. 280 (2021), CrossRefGoogle Scholar
Guo, B. and Huang, D.. Existence and stability of standing waves for nonlinear fractional Schrödinger equations. J. Math. Phys. 53 (2012), .CrossRefGoogle Scholar
Hajaiej, H. and Song, L.. A general and unified method to prove the uniqueness of ground state solutions and the existence/non-existence, and multiplicity of normalized solutions with applications to various NLS. arXiv:2208.11862v3, (2023).Google Scholar
Hirata, J. and Tanaka, K.. scalar field equations with L 2 constraint: mountain pass and symmetric mountain pass approaches. Adv. Nonlinear Stud. 19 (2019), 263–290.CrossRefGoogle Scholar
Jeanjean, L.. Existence of solutions with prescribed norm for semilinear elliptic equations. Nonlinear Anal. 28 (1997), 1633–1659.CrossRefGoogle Scholar
Jeanjean, L. and Lu, S.. Nonradial normalized solutions for nonlinear scalar field equations. Nonlinearity 32 (2019), 4942–4966.CrossRefGoogle Scholar
Kirkpatrick, K., Lenzmann, E. and Staffilani, G.. On the continuum limit for discrete NLS with long-range lattice interactions. Comm. Math. Phys. 317 (2013), 563–591.CrossRefGoogle Scholar
Laskin, N.. Fractional quantum mechanics and Lévy path integrals. Phys. Lett. A 268 (2000), 298–305.CrossRefGoogle Scholar
Le Coz, S.. A note on Berestycki-Cazenave’s classical instability result for nonlinear Schrödinger equations. Adv. Nonlinear Stud. 8 (2008), 455–463.CrossRefGoogle Scholar
Li, Z., Zhang, Q. and Zhang, Z.. Stable standing waves of nonlinear fractional Schrödinger equations. Commun. Pure Appl. Anal. 21 (2022), 4113–4145.CrossRefGoogle Scholar
Li, Z., Zhang, Q., and Zhang, Z.. Standing waves of fractional Schrödinger equations with potentials and general nonlinearities. Anal. Theory Appl. 39 (2023), 357–377.Google Scholar
Lions, P. -L.. The concentration-compactness principle in the calculus of variations. The locally compact case. I. Ann. Inst. Ann. Inst. H. Poincaré Anal. Non LinéAire. 1 (1984), 109–145.CrossRefGoogle Scholar
Lions, P. -L.. The concentration-compactness principle in the calculus of variations. The locally compact case. II. Ann. Inst. H. Poincaré Anal. Non LinéAire. 1 (1984), 223–283.CrossRefGoogle Scholar
Liu, Z., Luo, H. and Zhang, Z.. Dancer-Fucccik spectrum for fractional Schrödinger operators with a steep potential well on $\mathbb{R}^N$. Nonlinear Anal. 189 (2019), .CrossRefGoogle Scholar
Luo, H. and Wu, D.. Normalized ground states for general pseudo-relativistic Schrödinger equations. Appl. Anal. 101 (2022), 3410–3431.CrossRefGoogle Scholar
Luo, H. and Zhang, Z.. Normalized solutions to the fractional Schrödinger equations with combined nonlinearities. Calc. Var. Partial Differ. Equ. 59 (2020), .CrossRefGoogle Scholar
Luo, H. and Zhang, Z.. Existence and stability of normalized solutions to the mixed dispersion nonlinear Schrödinger equations. Electron. Res. Arch. 30 (2022), 2871–2898.CrossRefGoogle Scholar
Luo, X., Yang, T. and Yang, X.. Multiplicity and asymptotics of standing waves for the energy critical half-wave. arXiv:2102.09702v1 (2021).Google Scholar
Peng, C. and Shi, Q.. Stability of standing wave for the fractional nonlinear Schrödinger equation. J. Math. Phys. 59 (2018), .CrossRefGoogle Scholar
Servadei, R. and Valdinoci, E.. The Brezis-Nirenberg result for the fractional Laplacian. Trans. Amer. Math. Soc. 367 (2015), 67–102.CrossRefGoogle Scholar
Shibata, M.. Stable standing waves of nonlinear Schrödinger equations with a general nonlinear term. Manuscripta Math. 143 (2014), 221–237.CrossRefGoogle Scholar
Soave, N.. Normalized ground states for the NLS equation with combined nonlinearities. J. Differ. Equ. 269 (2020), 6941–6987.CrossRefGoogle Scholar
Soave, N.. Normalized ground states for the NLS equation with combined nonlinearities: the Sobolev critical case. J. Funct. Anal. 279 (2020), .CrossRefGoogle Scholar
Yan, S., Yang, J. and Yu, X.. Equations involving fractional Laplacian operator: compactness and application. J. Funct. Anal. 269 (2015), 47–79.CrossRefGoogle Scholar
Zhang, Z.. Variational, Topological, and Partial Order Methods With Their Applications (Springer, Heidelberg, 2013).CrossRefGoogle Scholar
Zhen, M. and Zhang, B.. Normalized ground states for the critical fractional NLS equation with a perturbation. Rev. Mat. Complut. 35 (2022), 89–132.CrossRefGoogle Scholar
Zhu, S.. Existence of stable standing waves for the fractional Schrödinger equations with combined nonlinearities. J. Evol. Equ. 17 (2017), 1003–1021.CrossRefGoogle Scholar