Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T01:38:41.362Z Has data issue: false hasContentIssue false
  • English
  • Français

Inequalities for the tail probabilities of weighted sums of independent random variables with applications to rates of convergence to zero

Published online by Cambridge University Press:  14 November 2011

J. E. A. Dunnage
J. E. A. Dunnage
Affiliation:
Chelsea College (University of London), London SW3 6LX
Get access Rights & Permissions [Opens in a new window]

Synopsis

We obtain inequalities for 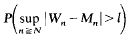where Wn = anlX1 + … + annXn, the Xr being independent random variables and the Mn being certain truncated means. We then use these inequalities to study the rate at which this probability tends to zero as N→ ∞, noting that in the special case Wn = (X1 + … + Xn)/n, we obtain the estimate given by L. E. Baum and M. Katz which they show is, in a sense, best possible.

A desire to find an inequality which would lead to the result of Baum and Katz was, indeed, the impetus behind this paper.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 93 , Issue 1-2 , 1982 , pp. 111 - 121
Copyright
Copyright © Royal Society of Edinburgh 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Baum, L. E. and Katz, M.. Convergence rates in the law of large numbers. Trans. Amer. Math. Soc. 120 (1965), 108–23.CrossRefGoogle Scholar
2Dunnage, J. E. A.. Analogues of the Kolmogorov and Hájek-Rényi inequalities with some applications to laws of large numbers. Quart. J. Math. Oxford 24 (1973), 273–88.CrossRefGoogle Scholar
3Dunnage, J. E. A.. Further analogues of the Kolmogorov and Hájek-Rényi inequalities with applications to rates of convergence to zero. Quart. J. Math. Oxford 26 (1975), 361–76.CrossRefGoogle Scholar
4Fuk, D. K.. Some probabilistic inequalities for martingales. Sibirsk. Mat. Ž. 14 (1973), 185–93. (English translation, Siberian Math. J. 14 (1973), 131–37.)Google Scholar
5Hájek, J. and Rényi, A.. Generalisations of an inequality of Kolmogorov. Acad. Math. Acad. Sci. Hungar. 6 (1955), 281–83.CrossRefGoogle Scholar