Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-24T08:55:15.437Z Has data issue: false hasContentIssue false
  • English
  • Français

Incompressible limit for the two-dimensional isentropic Euler system with critical initial data

Published online by Cambridge University Press:  01 December 2014

Taoufik Hmidi  and
Samira Sulaiman
Taoufik Hmidi
Affiliation:
Mathematics Research Institute of Rennes, Université de Rennes 1, Campus de Beaulieu, 35 042 Rennes Cedex, France, ([email protected])
Samira Sulaiman
Affiliation:
Mathematics Research Institute of Rennes, Université de Rennes 1, Campus de Beaulieu, 35 042 Rennes Cedex, France, ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

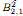We study the low-Mach-number limit for the two-dimensional isentropic Euler system with ill-prepared initial data belonging to the critical Besov space . By combining Strichartz estimates with the special structure of the vorticity, we prove that the lifespan of the solutions goes to infinity as the Mach number goes to zero. We also prove strong convergence results of the incompressible parts to the solution of the incompressible Euler system.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 144 , Issue 6 , December 2014 , pp. 1127 - 1154
Copyright
Copyright © Royal Society of Edinburgh 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)