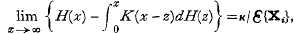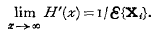Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Morimura, Hidenori
1956.
On a renewal theorem.
Kodai Mathematical Journal,
Vol. 8,
Issue. 3,
Klein, M.
and
Rosenberg, L.
1960.
Deterioration of inventory and equipment.
Naval Research Logistics Quarterly,
Vol. 7,
Issue. 1,
p.
49.
Hatori, Hirohisa
1961.
Some theorems in an extended renewal theory. III..
Kodai Mathematical Journal,
Vol. 13,
Issue. 4,
Matthes, Klaus
1962.
Ergodizitätseigenschaften rekurrenter Ereignisse. I.
Mathematische Nachrichten,
Vol. 24,
Issue. 2,
p.
109.
White, John S.
1964.
Weibull Renewal Analysis.
Vol. 1,
Issue. ,
Akulinichev, N. M.
and
Gorskii, L. K.
1975.
Asymptotic distributions of outgoing flows in queueing systems.
Cybernetics,
Vol. 9,
Issue. 1,
p.
83.
Birolini, Alessandro
1997.
Zuverlässigkeit von Geräten und Systemen.
p.
252.
Crane, Edward
Georgiou, Nicholas
Volkov, Stanislav
Wade, Andrew R.
and
Waters, Robert J.
2011.
The simple harmonic urn.
The Annals of Probability,
Vol. 39,
Issue. 6,
Annunziato, M.
Brunner, H.
and
Messina, E.
2012.
Asymptotic stability of solutions to Volterra-renewal integral equations with space maps.
Journal of Mathematical Analysis and Applications,
Vol. 395,
Issue. 2,
p.
766.
Maghsoodloo, Saeed
and
Helvaci, Dilcu
2014.
Renewal and Renewal-Intensity Functions with Minimal Repair.
Journal of Quality and Reliability Engineering,
Vol. 2014,
Issue. ,
p.
1.
Moffitt, Jeffrey R.
and
Bustamante, Carlos
2014.
Extracting signal from noise: kinetic mechanisms from a Michaelis–Menten‐like expression for enzymatic fluctuations.
The FEBS Journal,
Vol. 281,
Issue. 2,
p.
498.
Mitov, Kosto V.
and
Omey, Edward
2014.
Renewal Processes.
p.
1.
Wierenga, Harmen
ten Wolde, Pieter Rein
and
Becker, Nils B.
2018.
Quantifying fluctuations in reversible enzymatic cycles and clocks.
Physical Review E,
Vol. 97,
Issue. 4,
Kumar, Ashutosh
Adhikari, R.
and
Dua, Arti
2021.
Transients generate memory and break hyperbolicity in stochastic enzymatic networks.
The Journal of Chemical Physics,
Vol. 154,
Issue. 3,
Gutierrez, Miguel
and
Rivera, Francisco A.
2021.
Undershoot and order quantity probability distributions in periodic review, reorder point, order-up-to-level inventory systems with continuous demand.
Applied Mathematical Modelling,
Vol. 91,
Issue. ,
p.
791.
Hu, Miao
Wu, Di
Wu, Weigang
Cheng, Julian
and
Chen, Min
2022.
Quantifying the Influence of Intermittent Connectivity on Mobile Edge Computing.
IEEE Transactions on Cloud Computing,
Vol. 10,
Issue. 1,
p.
619.
Dallon, J. C.
Evans, Emily
Grant, Christopher P.
and
Portet, Stephanie
2024.
Steady state distributions of moving particles in one dimension: with an eye towards axonal transport.
Journal of Mathematical Biology,
Vol. 89,
Issue. 5,
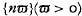 it is termed a discrete renewal process. The greatest k such that X1 + X2 + … + Xk ≤ x(> o) is a random variable N(x) and theorems concerning N(x) are renewal theorems. This paper is concerned with the proofs of a number of renewal theorems, the main emphasis being on processes which are not discrete. It is assumed throughout that the {Xi} are independent and identically distributed.
it is termed a discrete renewal process. The greatest k such that X1 + X2 + … + Xk ≤ x(> o) is a random variable N(x) and theorems concerning N(x) are renewal theorems. This paper is concerned with the proofs of a number of renewal theorems, the main emphasis being on processes which are not discrete. It is assumed throughout that the {Xi} are independent and identically distributed.