Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-06T10:53:07.587Z Has data issue: false hasContentIssue false
  • English
  • Français

Higher monotonicity properties of certain Sturm-Liouville functions. V†

Published online by Cambridge University Press:  14 February 2012

M. E. Muldoon
M. E. Muldoon
Affiliation:
Department of Mathematics, York University, Downsview, Ontario, Canada
Get access Rights & Permissions [Opens in a new window]

Synopsis

The principal concern here is with conditions on f or on special solutions of the equation

which ensure that the higher differences of the zeros and related quantities of solutions of (1) are regular in sign. In particular, by choosing f(x)= 2v−2x1/v−2, it is shown that if ⅓ ≦|v|<½, then

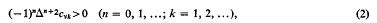
where cvk denotes the kth positive zero of a Bessel function of order v and Δµk = Δk+1 − µk. Lorch and Szego [15] conjectured that (2) should hold for the larger range | v | < ½ but the methods used here do not apply to the range | v <| ⅓.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 77 , Issue 1-2 , 1977 , pp. 23 - 37
Copyright
Copyright © Royal Society of Edinburgh 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Appell, P.Sur les transformations des équations différentielles linéaires. C.R. Hebd. Séanc. Acad. Sci. Paris 91 (1880), 211–214.Google Scholar
2Askey, R. Positive Jacobi polynomial sums, III. Linear operators and approximation, II. Internal. Ser. Num. Math. 25. Eds. Butzer, P. L. and Sz-Nagy, B. (Basel: Birkhäuser, 1974), 305–312.Google Scholar
3Cohn, J. H. E.Zeros of solutions of ordinary second order differential equations, II. J. London Math. Soc. 5 (1972), 53–58.Google Scholar
4Doetsch, G.Handbuch der Laplace-Transformation, II. (Basel: Birkhäuser, 1955).Google Scholar
5Duff, G. F. D.Positive elementary solutions and completely monotonic functions. J. Math. Anal. Appl. 27 (1969), 469–494.CrossRefGoogle Scholar
6Durand, L. Nicholson-type integrals for products of Gegenbauer functions and related topics. In Theory and application of special functions Ed. Askey, R. A. (New York: Academic Press, 1975), 352–374.Google Scholar
7Erdélyi, A. et al. Higher transcendental functions, 2 (New York: McGraw-Hill, 1953).Google Scholar
8Erdélyi, A. et al. Tables of integral transforms, 2 (New York: McGraw-Hill, 1954).Google Scholar
9Ferreira, E. M. and Sesma, J.Zeros of the modified Hankel function. Numer. Math. 16 (1970), 278–284.CrossRefGoogle Scholar
10Háčik, M.Contribution to the monotonicity of the sequence of zero points of integrals of the differential equation yn+q(t)y = 0 with regard to the basis [αβ;]. Arch. Math. (Brno) 8 (1972), 79–83.Google Scholar
11Háčik, M.Higher monotonicity properties of zero points of the linear combination of the solution and its first derivative of the differential equation yn+q(t)y = 0. Arch. Math. (Brno) 10 (1974), 67–78.Google Scholar
12Hartman, P.Differential equations and the function J2µ + Y2µ. Amer.J. Math. 83 (1961), 154–188.Google Scholar
13Hartman, P.On differential equations, Volterra equations and the function J2++. Amer. J. Math. 95 (1973), 553–593.CrossRefGoogle Scholar
14Hochstadt, H.The functions of mathematical physics (New York: Interscience, 1971).Google Scholar
15Lorch, L. and Szego, P.Higher monotonicity properties of certain Sturm-Liouville functions. Ada Math. 109 (1963), 55–73.Google Scholar
16Lorch, L. and Szego, P.Higher monotonicity properties of certain Sturm-Liouville functions, II. Bull. Acad. Polon. Sci. Ser. Sci. Math. Astronom. Phys. 11 (1963), 455–457.Google Scholar
17Lorch, L., Muldoon, M. E. and Szego, P.Higher monotonicity properties of certain Sturm-Liouville functions, III. Canad. J. Math. 22 (1970), 1238–1265.CrossRefGoogle Scholar
18Lorch, L., Muldoon, M. E. and Szego, P.Higher monotonicity properties of certain Sturm-Liouville functions, IV. Canad. J. Math. 24 (1972), 349–368.Google Scholar
19Meijer, C. S.Einige Integraldarstellungen für Produkte von Whittakerschen Funktionen. Quart. J. Math. Oxford Ser. 6 (1935), 241–248.Google Scholar
20Muldoon, M. E.Extension of a result of L. Lorch and P. Szego on higher monotonicity. Canad. Math. Bull. 11 (1968), 447–451.CrossRefGoogle Scholar
21Muldoon, M. E.Elementary remarks on multiply monotonic functions and sequences. Canad. Math. Bull. 14 (1971), 69–72.Google Scholar
22Vosmanský, J.The monotonicity of extremants of integrals of the differential equation yn+q(t)y = 0. Arch. Math. (Brno) 2 (1966), 105–111.Google Scholar
23Vosmanský, J.Monotonic properties of zeros and extremants of the differential equation yn+q(t)y = 0. Arch. Math. (Brno) 6 (1970), 37–74.Google Scholar
24Vosmanský, J.Certain higher monotonicity properties of ith derivatives of solutions of yn + a(t)y+b(t)y = 0. Arch. Math. (Brno) 10 (1974), 87–102.Google Scholar
25Watson, G. N.A treatise on the theory of Bessel functions 2nd edn (Cambridge: Univ. Press, 1944).Google Scholar
26Widder, D. V.The Laplace Transform (Princeton: Univ. Press, 1941).Google Scholar
27Wright, E. M.The asymptotic expansion of the generalized hypergeometric function. J. London Math. Soc. 10 (1935), 286–293.Google Scholar