Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-05T02:52:47.477Z Has data issue: false hasContentIssue false
  • English
  • Français

Gradient estimates for nonlinear elliptic equations with a gradient-dependent nonlinearity

Part of: Elliptic equations and systems Partial differential equations

Published online by Cambridge University Press:  30 January 2019

Joshua Ching  and
Florica C. Cîrstea
Joshua Ching
Affiliation:
School of Mathematics and Statistics, The University of Sydney, NSW 2006, Australia ([email protected]; [email protected])
Florica C. Cîrstea
Affiliation:
School of Mathematics and Statistics, The University of Sydney, NSW 2006, Australia ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we obtain gradient estimates of the positive solutions to weighted p-Laplacian type equations with a gradient-dependent nonlinearity of the form 0.1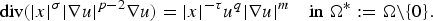

$${\rm div }( \vert x \vert ^\sigma \vert \nabla u \vert ^{p-2}\nabla u) = \vert x \vert ^{-\tau }u^q \vert \nabla u \vert ^m\quad {\rm in}\;\Omega^*: = \Omega {\rm \setminus }\{ 0\} .$$
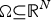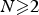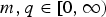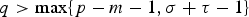Here, $\Omega \subseteq {\open R}^N$ denotes a domain containing the origin with $N\ges 2$, whereas $m,q\in [0,\infty )$, $1<p\les N+\sigma $ and $q>\max \{p-m-1,\sigma +\tau -1\}$. The main difficulty arises from the dependence of the right-hand side of (0.1) on x, u and $ \vert \nabla u \vert $, without any upper bound restriction on the power m of 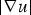$ \vert \nabla u \vert $. Our proof of the gradient estimates is based on a two-step process relying on a modified version of the Bernstein's method. As a by-product, we extend the range of applicability of the Liouville-type results known for (0.1).

Keywords

gradient boundsLiouville resultsa priori estimatesquasilinear elliptic equations

MSC classification

Primary: 35J62: Quasilinear elliptic equations
Secondary: 35B45: A priori estimates 35J75: Singular elliptic equations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 3 , June 2020 , pp. 1361 - 1376
Copyright
Copyright © 2019 The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Attouchi, A.. Gradient estimate and a Liouville theorem for a p-Laplacian evolution equation with a gradient nonlinearity. Differ. Integral Equ. 29 (2016), 137–150.Google Scholar
2Barles, G.. A weak Bernstein method for fully nonlinear elliptic equations. Differ. Integral Equ. 4 (1991), 241–262.Google Scholar
3Bernstein, S. N.. Sur la généralisation du problème de Dirichlet. I. Math. Ann. 62 (1906), 153–271.CrossRefGoogle Scholar
4Bernstein, S. N.. Méthode générale pour la resolution du problème de Dirichlet. C. R. Acad. Sci. Paris 144 (1907), 1025–1027.Google Scholar
5Bernstein, S. N.. Sur la généralisation du problème de Dirichlet. II. Math. Ann. 69 (1910), 82–136.CrossRefGoogle Scholar
6Bidaut-Véron, M. F., Garcia-Huidobro, M. and Véron, L.. Local and global properties of solutions of quasilinear Hamilton-Jacobi equations. J. Funct. Anal. 267 (2014), 3294–3331.CrossRefGoogle Scholar
7Chang, T.-Y. and Cîrstea, F. C.. Singular solutions for divergence-form elliptic equations involving regular variation theory: Existence and classification. Ann. Inst. H. Poincaré Anal. Non Linéaire 34 (2017), 1483–1506.CrossRefGoogle Scholar
8Ching, J. and Cîrstea, F. C.. Existence and classification of singular solutions to nonlinear elliptic equations with a gradient term. Anal. PDE 8 (2015), 1931–1962.CrossRefGoogle Scholar
9Cîrstea, F. C. and Du, Y.. Isolated singularities for weighted quasilinear elliptic equations. J. Funct. Anal. 259 (2010), 174–202.CrossRefGoogle Scholar
10Farina, A. and Serrin, J.. Entire solutions of completely coercive quasilinear elliptic equations, II. J. Differ. Equ. 250 (2011), 4409–4436.CrossRefGoogle Scholar
11Friedman, A. and Véron, L.. Singular solutions of some quasilinear elliptic equations. Arch. Rational Mech. Anal. 96 (1986), 359–387.CrossRefGoogle Scholar
12Gilbarg, D. and Trudinger, N. S.. Elliptic Partial Differential Equations of Second Order, 2nd edn, Grundlehren der Math. Wissenschaften,vol. 224 (Berlin: Springer, 1983).CrossRefGoogle Scholar
13Ladyzhenskaya, O. A.. Solution of the first boundary problem in the large for quasi-linear parabolic equations. Trudy Moskov. Mat. Obsc. 7 (1958), 149–177 [Russian].Google Scholar
14Ladyzhenskaya, O. A. and Ural'tseva, N. N.. Quasilinear elliptic equations and variational problems with several independent variables. Uspehi Mat. Nauk. 16 (1961), 19–90 [Russian]. English translation in Russian Math. Surveys 16 (1961), 17–92.Google Scholar
15Ladyzhenskaya, O. A. and Ural'tseva, N. N.. Linear and quasilinear elliptic equations, Moscow, Izdat. ‘Nauka’, 1964 [Russian]. English Translation, 2nd Russian edn, 1973 (New York: Academic Press, 1968).Google Scholar
16Lions, P. L.. Quelques remarques sur les problèmes elliptiques quasilinéaires du second ordre. J. Analyse Math. 45 (1985), 234–254.CrossRefGoogle Scholar
17Marcus, M. and Nguyen, P.-T.. Elliptic equations with nonlinear absorption depending on the solution and its gradient. Proc. London Math. Soc. (3) 111 (2015), 205–239.CrossRefGoogle Scholar
18Nguyen, P.-T.. Isolated singularities of positive solutions of elliptic equations with weighted gradient term. Anal. PDE 9 (2016), 1671–1691.CrossRefGoogle Scholar
19Pucci, P. and Serrin, J.. The maximum principle. Progress in nonlinear differential equations and their applications,vol. 73 (Birkhäuser: Basel, 2007).CrossRefGoogle Scholar
20Serrin, J.. The problem of Dirichlet for quasilinear elliptic differential equations with many independent variables. Philos. Trans. Roy. Soc. London Ser. A 264 (1969), 413–496.Google Scholar
21Song, H., Yin, J. and Wang, Z.. Isolated singularities of positive solutions to the weighted p-Laplacian. Calc. Var. Partial Differ. Equ. 55 (2016), Art. 28, 16 pp. https://doi.org/10.1007/s00526-016-0971-1.CrossRefGoogle Scholar
22Tolksdorf, P.. Regularity for a more general class of quasilinear elliptic equations. J. Differ. Equ. 51 (1984), 126–150.CrossRefGoogle Scholar
23Trudinger, N. S.. On Harnack type inequalities and their application to quasilinear elliptic equations. Comm. Pure Appl. Math. 20 (1967), 721–747.CrossRefGoogle Scholar