General uniqueness results and blow-up rates for large solutions of elliptic equations
Published online by Cambridge University Press: 10 August 2012
Abstract
Making use of the Karamata regular variation theory and the López-Gómez localization method, we establish the uniqueness and asymptotic behaviour near the boundary ∂Ω for the large solutions of the singular boundary-value problem
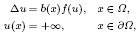
where Ω is a smooth bounded domain in ℝN. The weight function b(x) is a non-negative continuous function in the domain, which can vanish on the boundary ∂Ω at different rates according to the point x0 ∊ ∂Ω. f(u) is locally Lipschitz continuous such that f(u)/u is increasing on (0, ∞) and f(u)/up = H(u) for sufficiently large u and p > 1, here H(u) is slowly varying at infinity. Our main result provides a sharp extension of a recent result of Xie with f satisfying limu→f(u)/up = H for some positive constants H > 0 and p > 1.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 142 , Issue 4 , August 2012 , pp. 825 - 837
- Copyright
- Copyright © Royal Society of Edinburgh 2012
- 3
- Cited by


