Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Giaquinta, M.
1994.
First European Congress of Mathematics Paris, July 6–10, 1992.
Vol. 120,
Issue. ,
p.
49.
Hong, Min-Chun
1995.
The Landau-Lifshitz equation with the external field—a new extension for harmonic maps with values inS 2.
Mathematische Zeitschrift,
Vol. 220,
Issue. 1,
p.
171.
Isobe, Takeshi
1997.
Some new properties of Sobolev mappings: intersection theoretical approach.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 127,
Issue. 2,
p.
337.
Isobe, Takeshi
1998.
Energy estimate, energy gap phenomenon, and relaxed energy for Yang-Mills functional.
The Journal of Geometric Analysis,
Vol. 8,
Issue. 1,
p.
43.
Taheri, Ali
2005.
Local Minimizers and Quasiconvexity – the Impact of Topology.
Archive for Rational Mechanics and Analysis,
Vol. 176,
Issue. 3,
p.
363.


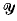 if
if 