Published online by Cambridge University Press: 16 May 2014
We consider the fractional derivative of a general Poisson semigroup. With this fractional derivative, we define the generalized fractional Littlewood–Paley g-function for semigroups acting on Lp-spaces of functions with values in Banach spaces. We give a characterization of the classes of Banach spaces for which the fractional Littlewood–Paley g-function is bounded on Lp-spaces. We show that the class of Banach spaces is independent of the order of derivation and coincides with the classical (Lusin-type/-cotype) case. We also show that the same kind of results exist for the case of the fractional area function and the fractional gλ*-function on ℝn. Finally, we consider the relationship of the almost sure finiteness of the fractional Littlewood–Paley g-function, the area function and the gλ*-function with the Lusin-cotype property of the underlying Banach space. As a byproduct of the techniques developed, one can find some results of independent interest for vector-valued Calderón–Zygmund operators. For example, one can find the following characterization: a Banach space 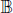 is the unconditional martingale difference if and only if, for some (or, equivalently, for every) p ∈ [1, ∞),
is the unconditional martingale difference if and only if, for some (or, equivalently, for every) p ∈ [1, ∞), 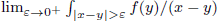 dy exists for almost every x ∈ ℝ and every
dy exists for almost every x ∈ ℝ and every 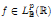 .
.