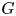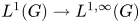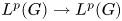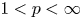Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hong, Qing
and
Hu, Guorong
2024.
Extended Abstracts 2021/2022.
Vol. 2,
Issue. ,
p.
57.
Ghosh, Abhishek
and
Ruzhansky, Michael
2024.
Sparse bounds for oscillating multipliers on stratified groups.
Monatshefte für Mathematik,
Vol. 205,
Issue. 3,
p.
511.
Cardona, DuvÁn
Delgado, Julio
and
Ruzhansky, Michael
2024.
Boundedness of the dyadic maximal function on graded Lie groups.
The Quarterly Journal of Mathematics,
Vol. 75,
Issue. 3,
p.
809.